-
 Git LFS (Large File Storage) 사용하기
Git의 용량제한과 LFS기본적으로 git은 여러개의 작은 소스코드 파일들을 위한 버전 컨트롤 시스템(VCS)이다. 따라서 Github의 경우 50Mb부터 Warning이 표시되고, 100Mb부터는 push시 Error가 발생한다. 그럼에도 불구하고 경우에 따라서 반드시 대용량 파일을 git repo에 포함시켜야하는 상황이 존재할 수 있다(예를 들면 학습된 모델파라미터를 올려야할 때). 이러한 경우에 사용할 수 있는 해결책인 Git LFS(Large File Storage)을 소개한다. git lfs가 정상적으로 적용된 경우, 아주 큰 파일에 대해서도 git push와 pull이 가능해진다. 기본적인 사용방법은 다음 블로그에서 가져왔다.https://leimao.github.io/blog/Git-Larg..
2020.03.30
Git LFS (Large File Storage) 사용하기
Git의 용량제한과 LFS기본적으로 git은 여러개의 작은 소스코드 파일들을 위한 버전 컨트롤 시스템(VCS)이다. 따라서 Github의 경우 50Mb부터 Warning이 표시되고, 100Mb부터는 push시 Error가 발생한다. 그럼에도 불구하고 경우에 따라서 반드시 대용량 파일을 git repo에 포함시켜야하는 상황이 존재할 수 있다(예를 들면 학습된 모델파라미터를 올려야할 때). 이러한 경우에 사용할 수 있는 해결책인 Git LFS(Large File Storage)을 소개한다. git lfs가 정상적으로 적용된 경우, 아주 큰 파일에 대해서도 git push와 pull이 가능해진다. 기본적인 사용방법은 다음 블로그에서 가져왔다.https://leimao.github.io/blog/Git-Larg..
2020.03.30
-
라즈베리파이 OS 포멧/초기화/업데이트
라즈베리파이 OS 초기화하기라즈베리파이에서 특별한 초기화 기능을 제공하지는 않는다. 검색해보면 shift키를 누른 상태로 재부팅을 하라고 하는데, 암만해도 안된다.결국 OS초기화를 위한 방법은 간단하다. 라즈베리파이에서 Micro SD 카드를 뽑고, 컴퓨터에 연결한다음 SD카드를 포멧시키고 다시 운영체제 설치부터 시작하는 것이다. https://newsight.tistory.com/287https://kocoafab.cc/tutorial/view/299 Python 3.7.3 버전으로 되돌리기라즈베리파이 최신 이미지는 처음부터 python 3.7.3버전이 설치되어있다.그래서 berryconda를 사용중이라면, berryconda를 삭제해버리면 된다. python3 --version 을 입력해보자. Ras..
2020.06.21
-
 Python Multiprocessing 가이드
Multiprocessing 가이드공식 레퍼런스 문서를 참고하여 작성하였다. 다음이 요소들이 multiprocessing의 가장 기본이고, 우선 이 네가지만 잘 알면된다. ProcessPoolQueuePipe Process단일 프로세스를 생성하는 경우, Process()를 사용한다. from multiprocessing import Process, Queuequeue = Queue()p = Process(target = my_function) #, args=(queue, 1))p.start()# p.join() # this blocks until the process terminates# result = queue.get()https://stackoverflow.com/questions/2046603/i..
2020.02.20
Python Multiprocessing 가이드
Multiprocessing 가이드공식 레퍼런스 문서를 참고하여 작성하였다. 다음이 요소들이 multiprocessing의 가장 기본이고, 우선 이 네가지만 잘 알면된다. ProcessPoolQueuePipe Process단일 프로세스를 생성하는 경우, Process()를 사용한다. from multiprocessing import Process, Queuequeue = Queue()p = Process(target = my_function) #, args=(queue, 1))p.start()# p.join() # this blocks until the process terminates# result = queue.get()https://stackoverflow.com/questions/2046603/i..
2020.02.20
-
 CSV파일 인코딩(Encoding)
CSV파일 인코딩(Encoding) 문제 해결하기 1. 현재 가지고 있는 csv파일에서 encoding이 무엇인지 알아내기 import chardet import pandas as pd filename = "Data_kr_v2.0.0_no_label_all_train3.csv" with open(filename, 'rb') as f: result = chardet.detect(f.readline()) # or read() if the file is small. print(result['encoding']) 이와 같은 방식으로 해당 라인의 encoding이 무엇인지 알아낼 수 있다. 2. Excel에서 csv 저장할 때 encoding변경하기 그런데 실제로 이렇게 옵션을 주고 해봐도, 제대로 encodin..
2020.03.23
CSV파일 인코딩(Encoding)
CSV파일 인코딩(Encoding) 문제 해결하기 1. 현재 가지고 있는 csv파일에서 encoding이 무엇인지 알아내기 import chardet import pandas as pd filename = "Data_kr_v2.0.0_no_label_all_train3.csv" with open(filename, 'rb') as f: result = chardet.detect(f.readline()) # or read() if the file is small. print(result['encoding']) 이와 같은 방식으로 해당 라인의 encoding이 무엇인지 알아낼 수 있다. 2. Excel에서 csv 저장할 때 encoding변경하기 그런데 실제로 이렇게 옵션을 주고 해봐도, 제대로 encodin..
2020.03.23
-
 딥러닝 프로젝트를 위한 클라우드 GPU 자원, Google Cloud Platform
GPU Cloud 서비스무료 GPU 서버현재까지 알려진 가장 좋은 무료 GPU 서비스는 Google colab이 유일하다. 그러나 colab은 하루에 12시간까지밖에 GPU를 쓸 수 없는 제약이 있고, 데이터를 지속적으로 서버에 올려둘 수가 없어서 google drive에 데이터를 올리고 이를 mount해서 사용해야하는데 이게 매우 불편하다. 또한 command line interface를 제공하지 않아서, jupyter의 cell에 !을 입력해서 해야하는데, 이 또한 매우 불편하다. 그리고 jupyter notebook도 기존에 사용하던 jupyter와 단축키 및 기능이 조금씩 달라서 적응하는데 꽤 시간이 걸린다. 그럼에도 불구하고 한시간에 1000원정도 하는 T4 GPU를 무료로 쓸 수 있다는 것은 ..
2019.12.08
딥러닝 프로젝트를 위한 클라우드 GPU 자원, Google Cloud Platform
GPU Cloud 서비스무료 GPU 서버현재까지 알려진 가장 좋은 무료 GPU 서비스는 Google colab이 유일하다. 그러나 colab은 하루에 12시간까지밖에 GPU를 쓸 수 없는 제약이 있고, 데이터를 지속적으로 서버에 올려둘 수가 없어서 google drive에 데이터를 올리고 이를 mount해서 사용해야하는데 이게 매우 불편하다. 또한 command line interface를 제공하지 않아서, jupyter의 cell에 !을 입력해서 해야하는데, 이 또한 매우 불편하다. 그리고 jupyter notebook도 기존에 사용하던 jupyter와 단축키 및 기능이 조금씩 달라서 적응하는데 꽤 시간이 걸린다. 그럼에도 불구하고 한시간에 1000원정도 하는 T4 GPU를 무료로 쓸 수 있다는 것은 ..
2019.12.08
-
 Coefficient of Determination(결정계수), R^2(R square)
결정계수 = Coefficient of Determination = R^2 = R squared - Regression model의 성능을 측정하기 위해 mean value로 예측하는 단순 모델(Zero-R 모델)과 비교해서, 상대적으로 얼마나 성능이 나오는지를 측정한 지표. (다른 성능 지표인 RMSE나 MAE는 데이터의 scale에 따라서 값이 천차만별이기 때문에, 절대 값만 보고 바로 성능을 판단하기가 어려운 반면, 결정계수의 경우 상대적 성능이기 때문에 보다 직관적으로 알 수 있다.) 결정계수(R^2) 구하는 공식 ( 보통의 경우 0
2017.05.22
Coefficient of Determination(결정계수), R^2(R square)
결정계수 = Coefficient of Determination = R^2 = R squared - Regression model의 성능을 측정하기 위해 mean value로 예측하는 단순 모델(Zero-R 모델)과 비교해서, 상대적으로 얼마나 성능이 나오는지를 측정한 지표. (다른 성능 지표인 RMSE나 MAE는 데이터의 scale에 따라서 값이 천차만별이기 때문에, 절대 값만 보고 바로 성능을 판단하기가 어려운 반면, 결정계수의 경우 상대적 성능이기 때문에 보다 직관적으로 알 수 있다.) 결정계수(R^2) 구하는 공식 ( 보통의 경우 0
2017.05.22
-
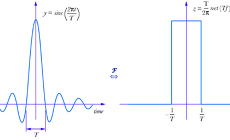 딥러닝과 FIR, IIR, LPF, HPF, BPF
Impulse responseImpulse response(IR), 혹은 impulse response function(IRF)라고 불리운다. 좀 더 직관적인 의미는 후자가 더 와닿는다. 이는 쉽게 말하면 어떠한 신호를 처리하는 system이 있을 때, input signal을 받아서 어떻게 output signal로 변형시키는지에 대한 함수(시간에 대한 함수)를 가리키는 말이다. 만약 우리가 어떤 공연장의 IR 데이터를 갖고 있으면, 어떠한 소리든지 그 공연장에서 나오는 소리처럼 변형시킬 수 있게 된다. # 용어 - Impulse: input signal을 의미함 - response: output signal을 의미함 Impulse(unit impulse)출처: https://en.wikipedia.o..
2014.07.01
딥러닝과 FIR, IIR, LPF, HPF, BPF
Impulse responseImpulse response(IR), 혹은 impulse response function(IRF)라고 불리운다. 좀 더 직관적인 의미는 후자가 더 와닿는다. 이는 쉽게 말하면 어떠한 신호를 처리하는 system이 있을 때, input signal을 받아서 어떻게 output signal로 변형시키는지에 대한 함수(시간에 대한 함수)를 가리키는 말이다. 만약 우리가 어떤 공연장의 IR 데이터를 갖고 있으면, 어떠한 소리든지 그 공연장에서 나오는 소리처럼 변형시킬 수 있게 된다. # 용어 - Impulse: input signal을 의미함 - response: output signal을 의미함 Impulse(unit impulse)출처: https://en.wikipedia.o..
2014.07.01
-
 Decibel과 SPL(Sound Pressure Level)
Decibel과 Sound Pressure Level(SPL)우선 벨은 단순히 P2과 P1의 비율에 log_10을 취한 것으로 두 값의 상대적인 비율을 나타내는 값이다. 보통 분자인 P2는 output signal을 의미하고, P1은 input signal을 의미한다.그다음 데시벨은 벨에서 1/10을 한 값이다. 보통의 경우 그냥 Bel은 너무나 큰 값이라서 쓰기가 매우 불편하다. 3 Bel 만해도 1000배를 의미하기 때문에 실제로 사용하려면 소수점이 발생하기 쉽다. 그래서 여기에 1/10을 곱해서 30 dB가 1000배를 의미하도록 만든 것이 바로 데시벨이다. 또한 데시벨은 기본적으로 log_10 을 사용하므로, 데시벨 수치가 +10 씩 증가할 때마다 실제 값은 기준치의 10배씩 증가하게 된다. (물..
2020.12.22
Decibel과 SPL(Sound Pressure Level)
Decibel과 Sound Pressure Level(SPL)우선 벨은 단순히 P2과 P1의 비율에 log_10을 취한 것으로 두 값의 상대적인 비율을 나타내는 값이다. 보통 분자인 P2는 output signal을 의미하고, P1은 input signal을 의미한다.그다음 데시벨은 벨에서 1/10을 한 값이다. 보통의 경우 그냥 Bel은 너무나 큰 값이라서 쓰기가 매우 불편하다. 3 Bel 만해도 1000배를 의미하기 때문에 실제로 사용하려면 소수점이 발생하기 쉽다. 그래서 여기에 1/10을 곱해서 30 dB가 1000배를 의미하도록 만든 것이 바로 데시벨이다. 또한 데시벨은 기본적으로 log_10 을 사용하므로, 데시벨 수치가 +10 씩 증가할 때마다 실제 값은 기준치의 10배씩 증가하게 된다. (물..
2020.12.22
-
 음성인식 기초 이해하기
# 발음기호와 문자표현 - phoneme: 음소, 가장 작은 소리의 단위. 쉽게 말해 영어사전의 발음기호를 생각하면 된다. - grapheme: 자소(=문자소), 가장 작은 문자의 단위. 발음기호로 표현되기 이전의 원래 문자를 의미한다. 그리고 대부분의 경우 알파벳 1개가, phoneme 1개에 대응 된다. ex) help -> h / e / l / p 그러나 항상 phoneme과 1:1대응은 아니다. 예를 들어 shop 에서 sh는 2개의 알파벳이 묶어서 ʃ 으로 발음되므로, 2개의 알파벳이 1개의 grapheme에 대응 된다. ex) shop -> ʃ / ɑː / p 경우에 따라서 최대 4개의 알파벳이 1개의 graphpeme에 대응 되기도 한다. ex) weight -> w / ei / t - mo..
2019.12.29
음성인식 기초 이해하기
# 발음기호와 문자표현 - phoneme: 음소, 가장 작은 소리의 단위. 쉽게 말해 영어사전의 발음기호를 생각하면 된다. - grapheme: 자소(=문자소), 가장 작은 문자의 단위. 발음기호로 표현되기 이전의 원래 문자를 의미한다. 그리고 대부분의 경우 알파벳 1개가, phoneme 1개에 대응 된다. ex) help -> h / e / l / p 그러나 항상 phoneme과 1:1대응은 아니다. 예를 들어 shop 에서 sh는 2개의 알파벳이 묶어서 ʃ 으로 발음되므로, 2개의 알파벳이 1개의 grapheme에 대응 된다. ex) shop -> ʃ / ɑː / p 경우에 따라서 최대 4개의 알파벳이 1개의 graphpeme에 대응 되기도 한다. ex) weight -> w / ei / t - mo..
2019.12.29
-
 [구글 스콜라] 논문 검색 및 저자 검색
구글 스콜라 검색하기http://scholar.google.co.kr/ 구글은 세르게이 브린과 레리 페이지가 대학원 재학 중 개발한 검색 기술로 창업된 회사이다. 최초의 검색은 대학원에서의 논문 및 연구를 쉽게 찾아 중복된 연구를 막고 관련된 정보를 찾기 위한 특수한 목적에서 연구되었다. 검색 기술에는 상당히 복잡한 수학 이론이 들어가게 되는데, 당시 학계의 수학자들이 이러한 검색 엔진을 개발한다는 소식을 듣자 서비스의 필요성을 돕기 위해 자발적으로 참여하여 수학 이론을 발전시켰다고 한다. 즉 구글 스콜라는 구글이 만든 된 최초의 서비스고, 그것이 아직도 훌륭한 형태로 가장 좋은 학술 검색 엔진으로 쓰이고 있다. 위에 링크된 주소로 들어가면 아래와 같이 "거인의 어깨에 올라서서 더 넓은 세상을 바라보라-..
2014.04.28
[구글 스콜라] 논문 검색 및 저자 검색
구글 스콜라 검색하기http://scholar.google.co.kr/ 구글은 세르게이 브린과 레리 페이지가 대학원 재학 중 개발한 검색 기술로 창업된 회사이다. 최초의 검색은 대학원에서의 논문 및 연구를 쉽게 찾아 중복된 연구를 막고 관련된 정보를 찾기 위한 특수한 목적에서 연구되었다. 검색 기술에는 상당히 복잡한 수학 이론이 들어가게 되는데, 당시 학계의 수학자들이 이러한 검색 엔진을 개발한다는 소식을 듣자 서비스의 필요성을 돕기 위해 자발적으로 참여하여 수학 이론을 발전시켰다고 한다. 즉 구글 스콜라는 구글이 만든 된 최초의 서비스고, 그것이 아직도 훌륭한 형태로 가장 좋은 학술 검색 엔진으로 쓰이고 있다. 위에 링크된 주소로 들어가면 아래와 같이 "거인의 어깨에 올라서서 더 넓은 세상을 바라보라-..
2014.04.28
-
절전모드 해제 시 강제 재부팅이 되는 문제 해결
https://narie.tistory.com/328 컴퓨터 절전모드 재부팅되는 문제해결 컴퓨터 절전모드 해제(다시 켜짐) 문제 해결 어느 날 갑자기 컴퓨터 절전모드에서 다시 켜지는 경우가 생깁니다. 절전모드는 시간을 설정하면 그 시간에 컴퓨터가 자동으로 절전모드로 꺼집니 narie.tistory.com https://comeinsidebox.com/%EC%9C%88%EB%8F%84%EC%9A%B0-%EC%BB%B4%ED%93%A8%ED%84%B0-%EC%9E%90%EB%8F%99-%EC%9E%AC%EC%8B%9C%EC%9E%91-%EC%9E%90%EB%8F%99-%EC%9C%BC%EB%A1%9C-%EC%BC%9C%EC%A7%90-%EC%A1%B0%EC%B9%98-%ED%95%B4%EA%B2%B0/ 윈도..
2021.10.11
-
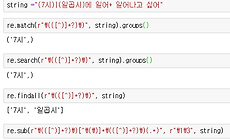 정규표현식, 정규식, 엑셀 고급기능
정규표현식(Regular Expression, Regex, 정규식) # 정규식 문법 - https://github.com/google/re2/wiki/Syntax - https://ko.wikipedia.org/wiki/%EC%A0%95%EA%B7%9C_%ED%91%9C%ED%98%84%EC%8B%9D # 복잡한 정규식의 사용에 대해 - 너무 심각하게 복잡한 기능이 필요한 정규식은 쓰지 말고, 그냥 python 프로그래밍으로 해결 하는 것이 훨씬 나은 방법이다. 그러나 정말 어쩔 수 없이 해야만한다면 정규식에 대한 매우 높은 이해도가 필요하다. - Python을 쓴다면, 정규식보다 훨씬 더 구현이 빠르고 정확하며, 디버깅, 유지보수, 협업이 용이해진다. 특히 너무 복잡한 문제에는 가능한 정규식은 사용하지..
2014.06.17
정규표현식, 정규식, 엑셀 고급기능
정규표현식(Regular Expression, Regex, 정규식) # 정규식 문법 - https://github.com/google/re2/wiki/Syntax - https://ko.wikipedia.org/wiki/%EC%A0%95%EA%B7%9C_%ED%91%9C%ED%98%84%EC%8B%9D # 복잡한 정규식의 사용에 대해 - 너무 심각하게 복잡한 기능이 필요한 정규식은 쓰지 말고, 그냥 python 프로그래밍으로 해결 하는 것이 훨씬 나은 방법이다. 그러나 정말 어쩔 수 없이 해야만한다면 정규식에 대한 매우 높은 이해도가 필요하다. - Python을 쓴다면, 정규식보다 훨씬 더 구현이 빠르고 정확하며, 디버깅, 유지보수, 협업이 용이해진다. 특히 너무 복잡한 문제에는 가능한 정규식은 사용하지..
2014.06.17
-
Precision의 의미
- bf16: 표현할 수 있는 값의 범위가 훨씬 넓은 대신, 숫자의 정밀한 표현이 어려움 loss underflow에 대해서 상당히 robust함 - fp16: 표현할 수 있는 값의 범위가 아주 아주 좁은 넓은 대신, 숫자를 정밀하게 표현할 수 있음 loss underflow가 일어나지 않는 경우에 훨씬 더 정확한 학습/추론이 가능함. fp16이든 bf16이든 모두 다 0에 가까운 숫자일 수록 정밀하게 표현할 수 있지만, 0에서 멀어질수록 점점 더 표현의 정밀도가 낮아질 수 있음. 그런데 bf16은 0에 가까운 숫자를 표현할 때의 정밀도는 더 떨어지지만, 더 넓은 범위를 표현할 수 있어서 loss explosion이나 NaN 문제에 있어서 robust함
2024.02.02
-
T-Test에 대한 이해
scikit learn에는 두가지 종류의 t-test가 구현되어 있다. 하나는 ttest_ind이고, 다른하나는 ttest_rel이다. 전자는 두 종류의 sample들이 완전히 독립적으로 추출되었을 때를 가정하고, 후자의 경우 그 반대를 의미한다. T-test의 구체적인 계산 과정은 아래와 같다. https://diseny.tistory.com/entry/t-test-%EB%B0%91%EB%B0%94%EB%8B%A5%EB%B6%80%ED%84%B0-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0 즉, 각 분포에서 뽑은 sample들의 차이들의 평균을 구해서 빼주고, 그리고 분모에 해당하는 모집단의 분산은 직접 구할수가 없기 때문에, 각 sample들의 분산을 구한다음 합쳐서 사용하는 방..
2024.02.02
-
확률 통계에서 분포에 대해 말하는 모드(Mode)란
https://dawoum.ddns.net/wiki/Mode_(statistics)
2023.08.21
-
Python Traceback 에러 로그에 표시되는 line이 부정확할 때
https://stackoverflow.com/questions/33175257/how-can-the-line-numbers-in-my-stack-traces-be-wrong How can the line numbers in my stack traces be wrong? I have a python (version 2.7.6) program that had been running for a day or two as of last night when it reported some errors. However, the stack traces were blatantly wrong. Pretend my code is like... stackoverflow.com 컴파일 시점의 python 소스코드와, 실제로 실..
2023.07.28
-
Kernel Density Estimation
https://darkpgmr.tistory.com/147 KDE는 히스토그램을 훨씬 고도화한 방법으로 이해할 수 있다. 각각의 x이 가우시안분포(커널)를 갖는다고 가정한다. 모든 점에 대해 가우시안분포를 부여한다음, 모든 확률을 누적해서 거대한 하나의 분포를 그린다. 즉, 히스토그램의 bin 대신 가우시안분포를 쓴다고보면 된다. Kernel Density Estimation(커널밀도추정)에 대한 이해 얼마전 한 친구가 KDE라는 용어를 사용하기에 KDE가 뭐냐고 물어보니 Kernel Density Estimation이라 한다. 순간, Kernel Density Estimation이 뭐지? 하는 의구심이 생겨서 그 친구에게 물어보니 자기도 잘 모른 darkpgmr.tistory.com
2023.07.26
-
윈도우 파일 중복 제거 무료 프로그램
https://zkim0115.tistory.com/1867 무료 중복 파일 삭제 프로그램 'Duplicate File Finder' PC내 중복 파일을 검색하고 필요없는 중복 파일을 삭제하는 무료 프로그램인 'Duplicate File Finder'입니다. 'Duplicate File Finder' 프로그램은 한국어 지원이 안되지만 단순히 중복 파일만을 검색하고 삭 zkim0115.tistory.com
2023.05.04
-
Equalizer APO 1.3
https://rdsong.com/3008 노트북 소리 키우기 - 컴퓨터 소리 증폭 프로그램 Equalizer APO 1.3 노트북 소리 키우는 프로그램 입니다. 노트북 소리 작아서 크게 올리는 프로그램 있는데 사용법도 간단합니다 노트북 컴퓨터 소리 증폭 하는 Equalizer APO 1.3 프로그램 사용 하면 됩니다.기본은 이 rdsong.com
2023.04.24
-
CCA(Canonical Correlation Analysis)
https://en.wikipedia.org/wiki/Canonical_correlation 두개의 vector를 각각 Linear Projection한다음 최대의 유사해지도록 가지도록 학습한 상태에서 corrleation을 구한것 SVCCA : SVD와 CCA를 결합 https://arxiv.org/abs/1706.05806
2023.03.21
-
Windows 10 단축키
https://blogs.windows.com/windows-insider/2014/10/03/keyboard-shortcuts-in-the-windows-10-technical-preview/ Keyboard Shortcuts in the Windows 10 Technical Preview Brad Sams asked me on Twitter yesterday if we had a list of new keyboard shortcuts in the Windows 10 Technical Preview. Here is what I was able to pull together for the keyboard junkies out there: Snapping window: WIN + LEFT or RIGHT ..
2022.07.22
-
CTC Beam Search
CTC 알고리즘 GT alignment가 없는 상황에서, 가장 그럴듯한 alignment를 학습하는 것 Forward Backward를 반복하면서, likelihood를 계산하고 maximize하는데, 이걸 계속해서 무한히 반복함으로써, 가장 그럴듯한 path들에 대한 확률을 높이는 것임 Full search하는 것에 대해서 계산량을 줄이기 위해서 dynamic programming을 한것 https://seunghyunseo.github.io/speech/2021/10/24/CTC/ CTC는 RNN이나 Transformer Decoder를 이용한 seq2seq이랑 전혀 다른 방식으로 생각을 해야한다. 모든 token에 대한 vocab probability를 BERT의 softmax(token featu..
2022.07.18
-
Python Module 실행
python -m ~~ https://jins-sw.tistory.com/22
2022.06.27
-
PPL 원리와 구현
PPL 원리와 구현 PPL이란 PPL의 정의는 기본적으로 target token seq에 대한 모델의 negative log-likelihood (NLL)의 평균을 exponential한 것이다. Perplexity of fixed-length models 계산 방법 PPL은 target data와 model prediction 사이의 CrossEntropy Loss를 exponentiation하여 매우 쉽게 계산할 할 수 있다. 이는 자명한 것이, model prediction과 target data (일종의 label로 생각)와의 CE를 계산하게 되면, target token의 index에 대한 model predction의 확률만으로 NLL이 계산되기 때문이다. $$ CrossEntropy(Mode..
2022.05.16
-
Contrastive Learning
Contrastive Learning Contrasitive Learning이 Masked Language Model하고 다른 핵심은, 감독학습처럼 명확하게 정답을 만들기 힘든 상황에서, ambiguous한 보기 중 가장 가까운 정답을 찾도록 하는 방식이라는 것이다. https://analyticsindiamag.com/contrastive-learning-self-supervised-ml/#:~:text=Contrastive%20learning%20is%20an%20approach,between%20similar%20and%20dissimilar%20images. Contrastive Learning에 쓰이는 Loss는 보통의 retreiver model 학습하는것처럼 CrossEntropy loss를..
2022.02.28
-
Hinge Loss
https://en.wikipedia.org/wiki/Hinge_loss Hinge Loss는 확률에 대한 정의가 들어있지 않으므로, 아주 쉽게 생각하면 일종의 regression 방식으로 학습된다고 생각할 수 있다. 즉 pos label에 대해서는 예측된 y값이 1로 수렴하도록 리그레션을 하는 것이다. 좀 더 정확히는 정답 class에 대해서는 1-y가 최소가 되도록 학습을 해서, y가 커지도록 학습이 되는건데 다만 y값이 무한히 커지면 안되니까 max(0, 1-y)를 취해서 y가 1보다 커지면 0으로 처리해버려서 1에서 멈추도록 한다. 즉 확률이란 가정없이 y의 범위가 1이하로 되도록 제한하는 것이다. 반면에 오답 class에 대해서는 1+y가 최소가 되어야하므로, y가 작아지도록 학습하는데, 이 역..
2022.01.06
-
절전모드 해제 시 강제 재부팅이 되는 문제 해결
https://narie.tistory.com/328 컴퓨터 절전모드 재부팅되는 문제해결 컴퓨터 절전모드 해제(다시 켜짐) 문제 해결 어느 날 갑자기 컴퓨터 절전모드에서 다시 켜지는 경우가 생깁니다. 절전모드는 시간을 설정하면 그 시간에 컴퓨터가 자동으로 절전모드로 꺼집니 narie.tistory.com https://comeinsidebox.com/%EC%9C%88%EB%8F%84%EC%9A%B0-%EC%BB%B4%ED%93%A8%ED%84%B0-%EC%9E%90%EB%8F%99-%EC%9E%AC%EC%8B%9C%EC%9E%91-%EC%9E%90%EB%8F%99-%EC%9C%BC%EB%A1%9C-%EC%BC%9C%EC%A7%90-%EC%A1%B0%EC%B9%98-%ED%95%B4%EA%B2%B0/ 윈도..
2021.10.11
-
How to fix ERR_UNSAFE_PORT error on Chrome when browsing to unsafe ports
https://superuser.com/questions/188006/how-to-fix-err-unsafe-port-error-on-chrome-when-browsing-to-unsafe-ports How to fix ERR_UNSAFE_PORT error on Chrome when browsing to unsafe ports I'm getting this error when connecting to a web server on port 6666 (http://myserver:6666/): Error 312 (net::ERR_UNSAFE_PORT): Unknown error. Is there an easy way to resolve this without rebuilding superuser.com
2021.09.28
-
Windows10에서 안드로이드 앱 실행하기
일반 버전의 BlueStacks을 설치하면, Hyper-V를 disable해야만 설치가 가능하다. 그러나 Windows Subsystem Linux (WSL)을 사용하는 중이라면, Hyper-V를 필수로 사용해야하기 때문에 불편하다. BlueStacks for Hyper-V 이 버전은 블루스택에서 공식적으로 제공하는 Hyper-V(베타)연동 버전이다. https://support.bluestacks.com/hc/en-us/articles/360049701852-Release-Notes-for-BlueStacks-Hyper-V-BETA- Release Notes for BlueStacks Hyper-V (BETA) BlueStacks version 4.280.0.4206 Download this versi..
2021.09.12
-
Ubuntu 20.04 고정 IP 할당 및 NetPlan으로 DNS설정하기
NetPlan 아마도 Ubuntu 18.04부터는 기존에 /etc/network/interfaces로 ip를 설정하던 방식에서, netplan과 yaml파일로 ip주소를 관리하는 방식으로 변경이 되었다. 따라서 기존에 방식 말고, 아래의 새로운 방식으로 설정해주어야 한다. 설정 방법 ip link : mac address 확인 cd /etc/netplan sudo cp 01-network-manager-all.yaml 01-network-manager-all.yaml.backup sudo vim 01-network-manager-all.yaml 아래와 같은 형식으로 주소를 입력한다. nameservers는 DNS 서버주소를 의미한다. 여기서 주의할 점은 띄어쓰기나, 들여쓰기 간격(탭이 아니라 띄어쓰기 2..
2021.07.01
-
Real Time C Programming
자료링크https://www.youtube.com/watch?v=N3XkQqhE6sY
2021.01.28
-
소리에 대한 사람의 인지적인 특성
Mel scalemel scale의 핵심은 사람이 멜로디를 인지하는 방식대로, hz에 대해 log scale을 취하겠다는 것이다. 데시벨소리의 크기인 amplitude를 log scale로 처리해주는 것. 이는 사람이 자극의 크기(소리의 크기)를 log scale로 인지하는 [베버-페히너의 법칙](https://ko.wikipedia.org/wiki/%EB%B2%A0%EB%B2%84-%ED%8E%98%ED%9E%88%EB%84%88%EC%9D%98_%EB%B2%95%EC%B9%99)에서 기초한다. https://m.blog.naver.com/PostView.nhn?blogId=msnayana&logNo=80100281096&proxyReferer=https:%2F%2Fwww.google.com%2F ht..
2021.01.07
-
 Decibel과 SPL(Sound Pressure Level)
Decibel과 Sound Pressure Level(SPL)우선 벨은 단순히 P2과 P1의 비율에 log_10을 취한 것으로 두 값의 상대적인 비율을 나타내는 값이다. 보통 분자인 P2는 output signal을 의미하고, P1은 input signal을 의미한다.그다음 데시벨은 벨에서 1/10을 한 값이다. 보통의 경우 그냥 Bel은 너무나 큰 값이라서 쓰기가 매우 불편하다. 3 Bel 만해도 1000배를 의미하기 때문에 실제로 사용하려면 소수점이 발생하기 쉽다. 그래서 여기에 1/10을 곱해서 30 dB가 1000배를 의미하도록 만든 것이 바로 데시벨이다. 또한 데시벨은 기본적으로 log_10 을 사용하므로, 데시벨 수치가 +10 씩 증가할 때마다 실제 값은 기준치의 10배씩 증가하게 된다. (물..
2020.12.22
Decibel과 SPL(Sound Pressure Level)
Decibel과 Sound Pressure Level(SPL)우선 벨은 단순히 P2과 P1의 비율에 log_10을 취한 것으로 두 값의 상대적인 비율을 나타내는 값이다. 보통 분자인 P2는 output signal을 의미하고, P1은 input signal을 의미한다.그다음 데시벨은 벨에서 1/10을 한 값이다. 보통의 경우 그냥 Bel은 너무나 큰 값이라서 쓰기가 매우 불편하다. 3 Bel 만해도 1000배를 의미하기 때문에 실제로 사용하려면 소수점이 발생하기 쉽다. 그래서 여기에 1/10을 곱해서 30 dB가 1000배를 의미하도록 만든 것이 바로 데시벨이다. 또한 데시벨은 기본적으로 log_10 을 사용하므로, 데시벨 수치가 +10 씩 증가할 때마다 실제 값은 기준치의 10배씩 증가하게 된다. (물..
2020.12.22
-
 Pytorch를 TensorRT로 변환해서 사용하기
TensorRT 설치과정TensoRT(trt)는 GPU inference 상황에서 최적의 optimization을 제공한다. 경우에 따라서는 거의 10배 이상 inference속도가 향상된다. 이 TensorRT를 사용하려면 조금 번거로운 설치과정을 해야한다. 그러나 설치만 잘 하면 변환 과정자체는 매우 쉽다. 1. CUDA 설치하기cuda 버전 10.2 ~ 11.1 까지 지원된다. 여기서는 CUDA 11.0 버전을 사용한다. 2. PyCUDA 설치하기pip install pycuda==2020.1 만약, CUDA를 새로 설치하거나 업데이트하면 pycuda역시 다시 재설치 or 업데이트가 필요하고 한다. 3. Pytorch 설치하기pytorch는 1.5.0부터 테스트되었으나, 그전 버전에서도 동작할 수 ..
2020.11.25
Pytorch를 TensorRT로 변환해서 사용하기
TensorRT 설치과정TensoRT(trt)는 GPU inference 상황에서 최적의 optimization을 제공한다. 경우에 따라서는 거의 10배 이상 inference속도가 향상된다. 이 TensorRT를 사용하려면 조금 번거로운 설치과정을 해야한다. 그러나 설치만 잘 하면 변환 과정자체는 매우 쉽다. 1. CUDA 설치하기cuda 버전 10.2 ~ 11.1 까지 지원된다. 여기서는 CUDA 11.0 버전을 사용한다. 2. PyCUDA 설치하기pip install pycuda==2020.1 만약, CUDA를 새로 설치하거나 업데이트하면 pycuda역시 다시 재설치 or 업데이트가 필요하고 한다. 3. Pytorch 설치하기pytorch는 1.5.0부터 테스트되었으나, 그전 버전에서도 동작할 수 ..
2020.11.25
-
Python Profiling
Line Profilerhttps://lothiraldan.github.io/2018-02-18-python-line-profiler-without-magic/python script를 한줄 단위로 profiling해줌 아래의 code snippets으로 쉽게 decorator로 구현 가능https://gist.github.com/kylegibson/6583590 cProfileimport cProfile, pstats, io from pstats import SortKey pr = cProfile.Profile() pr.enable() self.train_run() pr.disable() s = io.StringIO() sortby = SortKey.CUMULATIVE ps = pstats.Stats(..
2020.10.21
-
딥러닝을 위한 장비
한성컴퓨터 TFG257XG http://prod.danawa.com/info/?pcode=11258712 1.9키로인데 RTX2070이 달려있어서 딥러닝 학습도 가능하고, 발열제어가 뛰어나서 학습중에도 75도가 넘지 않는선으로 유지된다.(노트북 뒷판을 들어주는 거치대 사용시) 현재시점(2020년 9월)에서 유일하게 RTX2070 데스크탑버전이 쌩으로 달려있는 노트북이다. V100 한대당 10000달러 정도 하는 것으로 보인다. RTX3080 학습 속도는 V100과 거의 비슷한데, 가격은 700달러이다. 단, GPU RAM이 10Gb으로 매우 작다.
2020.09.21
-
AWS Jupyter setting
You need to DNS server registration with 8.8.8.8꼭 필요하진 않지만, 기본적으로 pip install등을 할 때 DNS를 못찾는 에러가 자주 발생하므로 구글 DNS서버를 등록해주자. sudo vim /etc/resolv.conf 를 하고, 아래 line을 추가해준다.nameserver 8.8.8.8 public jupyter notebook serverssl key를 만들고, 그것을 입력해서 jupyter 서버를 띄워야한다. https://docs.aws.amazon.com/dlami/latest/devguide/setup-jupyter-config.htmlhttps://docs.aws.amazon.com/dlami/latest/devguide/setup-jupyte..
2020.09.06
-
Python Callback
Callback Method Callback Method에 변수 전달 방법callback method에는 오직 global variable만이 전달될 수 있다. 만약 이것이 문제가 될 것 같다면 global variable만 가지고 있는 global class를 만들어서 이를 전달하는 방법이 좋다.https://stackoverflow.com/questions/51959978/how-to-pass-a-value-to-callback-for-anonymization-without-global-variables Callback 함수에 전역 변수를 전달하는 가장 효과적인 방법Singleton을 사용한다. 싱글톤은 전역변수이기 때문에 쉽게 callback에 전달 가능하고, 디자인도 깔끔해진다. https://n..
2020.08.13
-
 Python Subprocess
Subprocess VS Multi-processSubprocess는 python으로 다른 프로그램을 실행하기 위한 기능이다. 즉 단순히 system command를 실행하기 위함이라고 이해할 수 있다. 따라서 subprocess로 실행된 프로그램과는 오직 stdin/stdout만으로 통신 할 수 밖에 없다.반대로 multiprocess는 python 내에서 task를 쪼개 여러 cpu에서 실행하며, 좀 더 communication이 용이하다. Subprocess로 System Command 실행하기python에서 command line으로 명령을 내리는 방법은 os.system()을 이용하는 방법과, subprocess를 이용하는 방법 두가지가 있다. 그러나 여러가지 이유로 os.system()보다는 ..
2020.08.13
Python Subprocess
Subprocess VS Multi-processSubprocess는 python으로 다른 프로그램을 실행하기 위한 기능이다. 즉 단순히 system command를 실행하기 위함이라고 이해할 수 있다. 따라서 subprocess로 실행된 프로그램과는 오직 stdin/stdout만으로 통신 할 수 밖에 없다.반대로 multiprocess는 python 내에서 task를 쪼개 여러 cpu에서 실행하며, 좀 더 communication이 용이하다. Subprocess로 System Command 실행하기python에서 command line으로 명령을 내리는 방법은 os.system()을 이용하는 방법과, subprocess를 이용하는 방법 두가지가 있다. 그러나 여러가지 이유로 os.system()보다는 ..
2020.08.13
-
Smooth Approximation
LogSumExpLogSumExp는 max()의 smooth approximation이다.그 이유는 exp를 취하게 되면, 숫자가 큰 값의 영향력이 지수적으로 커지게 되는데, 이것들을 덧셈을 하게되면 숫자가 작은 값들은 영향력이 매우 줄어들게된다.그다음 log를 취해서 다시 exp의 역과정을 하게 되면, 사실상 영향력이 큰 숫자만 의미를 갖게 되므로 max함수와 유사한 기능을 하게 된다. https://en.wikipedia.org/wiki/LogSumExp Softmaxsoftmax는 argmax()의 smooth approximation이다.argmax의 결과물이 one-hot encoding으로 표현되는 상황에서 사실상 softmax의 결과물은 argmax와 같은 솔루션을 갖는다. 특히 temper..
2020.08.06
-
Python Function Result Caching by Joblib.Memory
Joblib.MemoryMemory를 이용하면 어떤 함수의 return 되는 output을 지정된 디렉토리에 저장해둔다. 그리고 해당 함수를 다시 호출할 경우, 미리 계산해둔 output을 가져와서 로딩을 하게 된다. 그리고 해당 cache는 사용자가 임의로 삭제하지 않으면 계속 유지되며, 다른 프로세스에서도 접근 가능하다고 한다.(확인 필요) 즉 이는 함수의 연산 결과를 하드디스크에 캐싱해두는 방식으로 볼 수 있다. 사용법은 매우 간단하여 아래와 같다. 내가 정의한 함수를 cache()에 전달하여 다시 사용하는 것이다. 이 방식은 output이 pkl로 저장된다. if cache: extract_feature = Memory("./cache", verbose=0).cache(extract_feature..
2020.07.24
-
레이더와 라이다
- 레이더(Radar): 전자기파를 방출하고 돌아오는 시그널을 통해 주변의 물체를 파악 - 라이다(Lidar): 레이저를 방출하고 돌아오는 시그널을 통해 주변의 물체를 파악레이저는 직진하도록 가지런히 모은 전자기파를 의미하며, 따라서 라이다는 레이더에 비해 더 고해상도이다. http://blog.naver.com/e_mobis/221979032096
2020.07.21












