Jacobian Matrix, Fisher Matrix, Hessian Matrix,

Jacobian Matrix

output이 1차원 실수인 함수를 n차원 벡터로 미분하면 자코비안(1*n)행렬이 된다.

output이 1차원 실수인 함수를 n차원 벡터로 2번 미분하면 헤시안(n*n)행렬이 나온다. 

(이는 자코비안을 한 다시 n짜리 벡터로 미분한 것과 같다.)

(행렬을 벡터가 아닌 스칼라로 미분할 때는 그냥 하나의 변수에 대해 미분하면 된다.)

 

여기서 맨 오른쪽의 matrix는 함수 f의 output이 1차원 실수일 때는 무시해도 된다.(맨 윗줄만 존재하는 것임.)

Jacobian Matrix : 어떤 행렬을 벡터 각각의 변수들로 차례차례 바꿔가면서 한 번 씩 미분한 행렬이다.

어떤 행렬의 성분에 대해
첫 번째 줄은 첫 번 째 성분에 대해 모든 변수들로 차례차례 한 번 씩 번갈아가면서 미분.
두 번째 줄은 두 번 째 성분에 대해 모든 변수들로 차례차례 한 번 씩 번갈아가면서 미분.
...
(그냥 행렬의 성분을 각 변수들로 순서대로 한 번 씩 미분한다고 생각.)

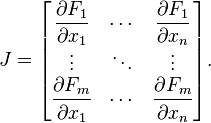
Ex) F(x,y)=(x^2+y)의 자코비안 메트릭스

Ex) F(x,y)=(x^2+y, 3x+5y)의 야코비안 메트릭스

참고 : 즉, Gradient Descent에서 Error를 계산할 때 아웃풋 변수가 1개인 함수를 각 파라미터에 대해 편미분을 하므로, 야코비안 행렬을 사용한다고 볼 수 있다.

Fisher Information Matrix

정의: gradient matrix의 covariance matrix

https://wiseodd.github.io/techblog/2018/03/11/fisher-information/

Hessian Matrix

어떤 함수를 각각의 변수들로 순서대로 바꿔가면서 2 번씩 미분한 값들.
첫째 줄은 첫 번 째 변수로 한 번 미분하고, 두번째 미분은 순서대로 2 번째, 2 번째, 3 번째... 으로 미분
둘째 줄은 두 번 째 변수로 한 번 미분하고, 두번째 미분은 순서대로 1 번째, 2 번째, 3 번째... 으로 미분
셋째 줄은 세 번 째 변수로 한 번 미분하고, 두번째 미분은 순서대로 1 번째, 2 번째, 3 번째... 으로 미분

Ex) F(x,y)의 헤시안 메트릭스

Ex) F(x,y,z)의 헤시안 메트릭스

http://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant

http://en.wikipedia.org/wiki/Hessian_matrix

Gram Matrix(Gramian Matrix)

쉽게 말해 어떤 vector(N x 1)가 주어졌을 때, 이 vector로 가득 채운 Matrix V를 다음과같이 곱하여 V^T x V을 해서 만든 것을 Gram Matrix(N x N)라고 한다.

즉 특정 vector가 자기 자신과 가질 수 있는 inner product space를 모두 게산한 것이라고 볼 수 있다.

https://en.wikipedia.org/wiki/Gramian_matrix