0. Convolutional Neural Networks의 Graph 해석
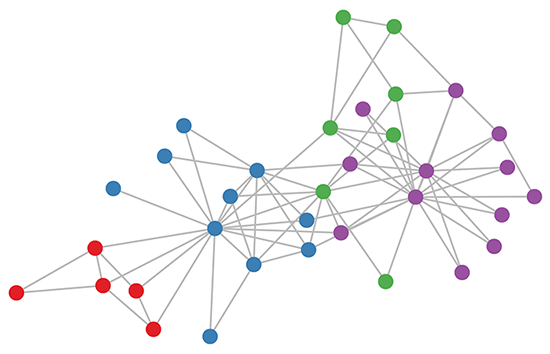
Karate club graph, colors denote communities obtained via modularity-based clustering
위와 같은 그래프 형태의 데이터를 학습하기 위한 가장 좋은 네트워크 아키텍쳐는 무엇일까? 바로 Graph Convolutional Networks이다.
GCN은 널리 알려진 Convolutional Neural Networks에 Adjacency Matrix를 도입하여 보다 데이터의 structure를 보다 일반화된 형태의 그래프로 정의한 것이다.
Adjacency Matrix란 아래와 같은 graph가 있을 때, 각 node간에 연결(edge)가 존재하면 1, 아니면 0으로 masking한 matrix를 의미한다. 즉 graph의 모양(topology)이 정의된 데이터이다.
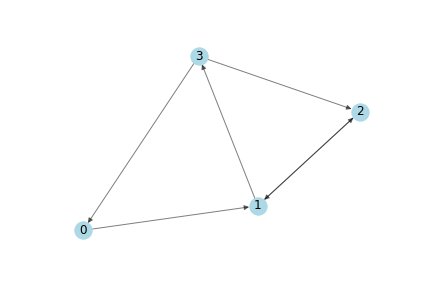
A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float)
이를 다시 설명하자면, CNN은 W*H 크기의 2차원 이미지가 주어졌을 때, 물리적으로 인접 픽셀들이 서로 topology(graph상에서 node와 edge의 연결이 존재)를 갖고 있다고 사전에 정의된 adjacency matrix를 가진 graph에 대한 convolution 연산으로 해석할 수 있다.
즉 2D CNN에서 정의하는 filter(kernel)의 사이즈가 만약 3x3이라면, 이는 이미지의 3*3개의 픽셀들이 전부 node이고, 각 node들이 자기자신을 포함해 인접한 주변 9개 픽셀들과 edge로 연결되어 있다는 의미이다.

https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md
보다 직관적인 이해를 위해 한가지 예제를 더 보자. 다음과 같이 만약 2D CNN의 filter가 WaveNet을 구현할 때 쓰이는 dilation=2을 갖는다면 어떨까?

이 경우 중앙 픽셀로부터 물리적으로 1칸의 간격을 두고서 node(픽셀)와 edge가 연결되어 있는 filter를 정의하게 된다. 즉 CNN의 filter의 모양을 정의하는 과정에서 이미 우리는 암묵적으로 Adjacency matrix가 정의된 그래프를 사용한 것이다.
1. Graph Convolutional Networks
이제 우리는 CNN이 암묵적 Graph에 대해 정의된 아키텍쳐임을 알고 있기 때문에, 이제 직관적으로 GCN을 이해하는 것이 어렵지 않다. GCN의 구현은 그냥 1x1 Convolution의 구조, 즉 주변의 node(픽셀)정보를 사용하지 않고, 오직 input channel에 대한 abstract feature를 추출한 다음, Adjacency Matrix(A)를 곱해서 주변 node의 정보를 합치게 된다. 만약 GCN의 A matrix가 identity matrix이라면, 이는 그냥 1x1 conv만 계속 쌓은 동치이다. (왜냐하면 1x1 conv처럼 각 픽셀에 대해서만 계산하고, windowing으로 weight sharing을 하기 때문이다. 좀 더 설명하자면 GCN의 W matrix는 𝐷∗𝐹 이고, input feature(D)를 output feature(F)로 보내는 linear embedding을 node N에 대해서 계속 반복하는 것이다.)
𝑓(𝐻(𝑙), 𝐴)=𝜎(𝐴 * 𝐻(𝑙) * 𝑊(𝑙))
다만, Adjacency Matrix는 원래 정의상, 대각행렬의 성분이 모두 0(즉, 자기자신과의 연결이 없음)이고 이것의 의미는 CNN의 filter에서 자기자신의 픽셀정보를 쓰지 않는 weight kernel이 생성되게 된다. 따라서 identity matrix를 더해준 𝐴=𝐴+𝐼 을 사용해서 문제를 해결한다.
더 나아가 feature normalization의 필요성, 그래프의 더 많은 정보를 전달하기 위한 Laplacian Matrix의 사용 등이 가능한데 이는 추후에 다시 다루기로 한다.

https://en.wikipedia.org/wiki/Laplacian_matrix
Adjacency Matrix를 곱하기만 했을 뿐인데 바로 GCN이 된다니 매우 놀랍지 않을 수 없다. 이것의 깊은 의미는 사실 직접 𝐴[𝑁∗𝑁]∗𝑋[𝑁∗𝐷] 의 매트릭스 곱셈을 직접 손으로 계산해보면 알 수 있는데, 말로 풀어서 설명하자면 자기 자신과 인접한 주변 node들의 feature(D)만 가져와서 weighted sum을 하겠다는 것이다. 즉 CNN에서의 3*3 filter가 하는 것처럼, 자기 자신의 인접 node(픽셀)들의 정보만 취합하여 sum을하고 non-linear activation을 거치는 것이 바로 Graph Convolution이다.
수식적으로는 다음과 같다.
𝐻𝑛𝑒𝑥𝑡[𝑁∗𝐹]=𝜎(𝐴[𝑁∗𝑁] ∗ 𝑋[𝑁∗𝐷] ∗ 𝑊[𝐷∗𝐹])
위 수식에서 먼저 𝑋[𝑁∗𝐷] ∗ 𝑊[𝐷∗𝐹]의 계산은 일반적인 linear embedding이다. 그러면 각 node가 가진 데이터를 D차원에서 F차원의 feature dimension으로 embedding할 수 있고, 여기에서 A를 곱하는 순간 각각의 node들은 자신과 1차적으로 연결된 node들의 feature를 sum해서 가져오는 filtering을 하게 된다. 그리고 나서 non-linear activation을 통과해 최종적인 계산을 하게 된다. 만약 이 layer를 계속해서 쌓는다면, 1차 연결된 node의 정보를 넘어서 N차 연결(N hop이라고도 한다.)된 node의 feature를 가져올 수 있게 된다. 즉 CNN에서도 층을 쌓을 수록 local feature에서 점점 global feature로 올라가듯이 GCN또한 전체 그래프에 대한 정보를 추출하게 된다.

https://raw.githubusercontent.com/wiki/alibaba/euler/images/GCN.png
여기서 핵심은 A를 곱하는 과정이 일종의 feature aggregation을 하는 과정인데, 이 부분은 Self-Attention과도 매우 밀접한 관련을 가지고 있다. 즉 Self-Attention은 임의의 Adjacency Matrix를 학습하는 아키텍쳐임라고 생각할 수 있다. 그렇다면 이 A matrix가 0 or 1의 binary가 아니라 실수값으로 빈도를 표현한다면 어떻게 될까? 또는 edge의 연결이 1종류가 아니라 여러가지 종류를 가진 heterograph라면 어떻게 해야할까? 추후 알아보도록 하자.
추가적으로, 그렇다면 GCN에 대한 아주 기본적인 베이스라인은 무엇일까? 𝑁∗𝐷의 input feature를 그냥 MLP에 집어넣는 것이고, 이는 각각의 node가 다른 모든 node와 fully connected되어 있다는 의미이다. 이는 마치 이미지를 CNN안쓰고 그냥 통째로 MLP에 넣는 것과 같다.
실험
이 GCN을 이용해 semi-supervised learning을 하면 가장 위에서 보았던 가라데 클럽 그래프가 다음과 같이 latent space상에서 feature들이 clustering되는 것을 볼 수 있다.
여기서의 semi-supervised learning은 가라데 클럽에 4가지 class가 존재하고(그래프의 색상), 각 class마다 속해있는 여러개의 node중에 딱 1개에만 labeling을 달아준 상태에서 다른 node들이 분류되도록 학습한 것이다. 데이터 중 일부에만 label이 존재하기 때문에 semi-supervised learing이 된다.
2. Graph Attention Networks(GATs)
기존의 GCN에서 Adjacency Matrix가 가진 binary값을 있는 그대로 사용하지 않고, 스스로 어떤 edge를 얼마나(실수값) 사용 할 지 결정할 수 있다. 이를 위해 masked-self multi-head attention을 도입한 것이 GATs이고, 이는 다음의 3가지 속성을 가진 (learnable/conditional/real-valued) Adjacency matrix를 만드는 것이 된다.

Self-attention은 다음의 과정을 통해 구해진다. 먼저 i번째 node와 j번째의 node의 feature에 W matrix를 곱해서(동일한 W를 재사용 즉, shared weight) linear embedding을 구한다. 이 둘을 concatenate해서 2F' dim의 데이터를 만든다. 그다음 이를 2F' 길이를 가진 learnable vector a(=single-layer, single hidden neural network)와 내적하여 𝑒𝑖𝑗 를 계산한다.
𝑒𝑖𝑗 는 i node와 인접한 j node의 importance를 의미한다. 이를 모든 node들 사이에(including self)에 대해서 계산하여 𝑁∗𝑁 크기의 E matrix를 만든다. 다만 이 과정에서 masking을 하게 되는데, 이는 원래 input으로 주어진 Adjacency matrix상에서 연결이 존재하는 edge들에 대해서만 𝑒𝑖𝑗 값을 계산하는 것을 의미한다.(추후 e값은 softmax에 사용되므로, 사실상 -999999와 같은 값을 넣으면 쉽게 masking 처리할 수 있다.)
그렇게 𝑁∗𝑁 사이즈의 E matrix를 만들고, 이를 row dimension에 대해서 각각 softmax를 취하여 𝑁∗1 의 attention이 계산된다.
이때 softmax를 취하는 과정의 분모는 i node와 인접한 j node들의 모든 𝑒𝑥𝑝(𝑒𝑖𝑗) 을 sum한 것이다. 즉 분모가 i node에 dependent한 값이 나오므로, 이 softmax의 계산 결과는 각 node를 기준으로 달라지게 된다.
즉 이는 attention은 각 node로 conditioning된 것이라고 말할 수 있고, 비유하자면 각 node들마다 서로 다른 A matrix가 있다고 해석 가능하고, 이는 edge가 node마다 다른 의미를 갖는다고도 확장할 수 있다. 실제로 논문에서는 다음과 같이 표현하고 있다.
... our model allows for (implicitly) assigning different importances to nodes of a same neighborhood ...
Multi-head attention을 적용해서, K개의 attention을 구하고(K개의 서로 다른 𝑊𝑘 가 존재함), 이렇게 구한 feature를 concatenate해서 사용한다.
계산 효율성 및 성능
그러나 단점으로는 PPNP 논문에서 속도를 비교한 결과 GAT가 매우 느리다고 보고되었다.

실험
- Transductive Learning: domain adaptation
Test X에 대한 정보(node와 graph structure)가 주어진 상황에서 test Y를 맞추는 문제
즉 test data의 모든 node들은 이미 training graph에 등장했던 node들이다. 즉 test graph가 training graph에 포함된 상황이다.
- Inductive Learning: supervised learning의 상황.
Test X에 대한 정보((node와 graph structure))가 전혀 주어지지 않은 상황에서 test Y를 맞추는 문제
Test data의 그 어떠한 정보도 알 수 없기 때문에, transductive learning 보다 test Y를 맞추기 훨씬 어렵다.
즉 test data의 node들은 단 한번도 training graph에는 등장한적이 없는 새로운 node들이다. 즉 test graph가 training graph에 포함되어있지 않은 상황이다.
=> Training에서는 본 적 없는 새로운 graph에 대해서 예측해야하는 문제이다. (test A matrix와 training A matrix가 서로 다르다.).

성능비교

https://github.com/alibaba/euler/wiki/%E6%95%88%E6%9E%9C%E6%B5%8B%E8%AF%95
GNN 구현 시 중요한 개념
# scipy.sparse 패키지 참조
- COO: COOrdinate format
(x,y)좌표와 그에 해당하는 value를 저장함. 그래서 ijv 포멧이라고도 함.
데이터를 저장하는 데 특화된 포맷으로, CSR이나 CSC로 변환하는 과정이 매우 빠르다.
대신 slicing이나 matrix multiplication 같은 연산이 불가능하므로, 이럴 때는 csr을 써야한다.
- CSR: Compressed Sparse Row format
다음과 같은 slicing이나,
csr_mat = csr_mat[nodes, :]
csr_mat = csr_mat[:, nodes]
다음과 같은 mm이 가능하다.
(torch.mm(adj, zk))
Advanced Question
- Adjacency Matrix를 이용한 mean pooling + 1x1 Conv로 이루어진 구조.
이것만 가지고 3x3 filter를 가진 CNN을 beating할 수 있을까?
- A matrix를 제곱하면 2-hop을 가져올 수 있다.
- 체비세프 폴리노미얼의 1차 근사이기 때문에 이렇게 1x1 conv만 주어진것이고, 그걸 아래 블로그에서 3x3 filter로 표현한게 파라미터가 1개이다 이렇게 연결되는 것 같다.
- inference블로그에 보면, 이 GCN에 대한 spectral domain에서의 해석과 한계점에 대해서 얘기하고 있다. 그러나 배경지식이 부족하여 온전히 내용을 이해하지 못해 참고문헌만 남긴다.
https://www.inference.vc/how-powerful-are-graph-convolutions-review-of-kipf-welling-2016-2/
Transformer의 GNN 해석
- 전체 vocab을 구성하는 각 word = node
- 1개의 sentence = 전체 그래프에서 fully connected 된 node들이 일부 subsampling된 subgraph
- self-attention = fully connected subgraph에 GAT를 적용한것
자연어에서 하나의 paragraph를 Inductive Learning setup에서의 GNN의 subgraph로 간주할 수 있다. 다만 차이점이라면 Transformer에서는 모든 subgraph의 edge들이 undirected fully connected graph라고 자동으로 가정이 되어있고, 이러한 fully connected edge들 중에서 무엇이 의미있는 edge인지를 학습하는 과정이 attention학습을 통해서 이뤄지는 것이다. 즉, 트랜스포머는 임의의 underlying graph structure를 학습하는 것이라고 말할 수 있다.
다만, GNN에는 graph에서 정보가 1 hop씩 propagation되는 개념이 있으나, Transformer에는 이러한 개념이 없이 한번에 전역으로 propagation이 된다는 차이가 있다.
다양한 주제
- 헤테로그래프에는 두가지가 종류가 있다.
1. 노드가 헤테로하다.
2. Edge가 헤테로하다.
그런데 이거를 한 번에 다룰 수 있는 방법이 A 매트릭스를 3차원, 4차원 텐서로 확장하는 것이다.
그래서 3번(N개)과 4번째(M개) dim을 하나씩 쪼개서 싱글 2차원 A 매트릭스를 학습한 node feature들이 N*M 가 나오는데, 이를 또 각각 N마다 attetion으로 요약, M마다 attention으로 요약
추천시스템의 inference속도 최적화
추천시스템(link prediction)의 Evaluation Metric
추천 시스템은 retrieval task 및 ranking task, metric learning과 아주 아주 밀접한 연관성을 가지고 있다.
- Data split
- Hit ratio과 MRR(Mean Reciprocal Rank)
Retrieval task에서 postitive label 1가지 밖에 없을 때 실무에서 성능을 측정하기 좋은 두 metric.
Top-K개의 후보 중에서 positive에 해당하는 item이 들어 있으면 True, 없으면 False로 acc를 계산하면 hit ratio가 된다.
여기서 더 나아가, MRR = 1/(positive item이 등장한 순서)으로 계산할 수 있고, TopK밖에서 positive가 등장하면 이때의 MRR은 0이 된다.
- Hit ratio의 문제
embedding과의 거리가 K rank안에 들면 1, 그 밖으로 나가면 0이기 때문에 Step function과 같은 boundary weighting을 가지고 있음. 그런데 이렇게 하면 극단적으로 말해 serendipity를 고려한 measure가 힘든데, 왜냐하면 정답의 기준이 되는 historical click sequence에는 비록 없었지만, 아주 nice한 더 좋은 추천을 많이 하는 새로운 알고리즘이 학습될 경우에 상위 K(8등 이라고 가정)등 안에 기존 추천 아이템이 들지 못하면 숫자가 0으로 나와버리기 때문이다. 그래서 이런 hard constraint를 사용할게 아니라 MRR과 같이 1/x 함수를 이용해 어느정도 부드럽게 weighting을 한 랭킹이 더 유효할 수 있다.
- MRR의 문제
그런데 또 MRR의 경우 역수의 모양을 유저가 마음대로 조절할 수 없는 문제와 동시에 사람이 해석하기 힘들다는 문제가 있다. 랭킹의 역수를 취한다음, 전체 평균을 계산하므로 이 모델은 1등, 9999등을 찾은 모델과 2등, 2등을 찾은 모델이 똑같은 값으로 나와 해석이 어렵다. 그리고 내 마음대로 커스터마이즈해서 weighting을 줄 수 없어서 보조적인 매트릭이 따로 필요하다. 예를 들어 지수함수의 모양을 커스터마이징 할 수 있는 MRR같은것이 필요하다. 가장 좋은 것은 랭킹의 histogram을 눈으로 확인하는 것이지만, 현실적으로 요약 통계치를 뽑아야하므로 문제 상황에 맞게 weighting을 해야한다.
- Hard negative
- Triplet loss
어떠한 기준점에 해당하는 anchor embedding이 있고, positive example의 embedding은 anchor와 거리가 가까워지고, negative example과는 거리가 멀어지도록 하는 loss를 학습하는 것.
추천시스템의 경우 anchor가 user embedding이고, positive item / negative item으로 뽑은 embedding을 사용한다. 이 때 negative item을 샘플링하여 사용하는데, 여기에 수 많은 휴리스틱 방법들이 존재한다. 예를 들어 hard negative를 정의해서 일정 비율이 섞이도록 하거나, 커리큘럼러닝처럼 점점 negative 난이도를 높이거나, positive에 perturbation을 주어 negative로 사용하거나 할 수 있다.
Loss에 들어가는 margin term을 이용하면 약간의 regularize효과를 줄 수 있으며, distance를 임의의 metric으로 정의할 수 있다. L2 norm을 쓸수도 있고 cosine distance도 사용 가능.
그리고 triplet loss로 학습한 embedding은 distance metric을 공유하는 ANN과 결합하여 retrieval 모델로 바로 사용이 가능한 장점이 있다.
References
- https://arxiv.org/abs/1609.02907
- https://tkipf.github.io/graph-convolutional-networks/
- https://arxiv.org/abs/1710.10903
Spectral GNN
본 글에서는 Spatial GNN에 대해 중점적으로 다루고 있다. GNN을 설명하는 또다른 축인 Spectral GNN에 대해서는 아래의 블로그 글을 참고하기 바란다.
- 라플라시안 Matrix
라플라시안행렬이 D+A가 아니라, D-A인 이유는 함축적으로 f(x+1)-f(x)의 의미를 가진다고 이해할 수 있다.
'Research > Deep Learning & Application' 카테고리의 다른 글
| Forward Looking Problem, Omniscient(Oracle) (0) | 2020.03.16 |
|---|---|
| 다양한 Convolution Layer (0) | 2020.01.30 |
| Residual connection (0) | 2019.10.22 |
| 각종 Normalization technique (2) | 2019.10.22 |
| 딥러닝에서 쓸만한 다양한 Ensemble Method (0) | 2018.11.01 |




댓글