P, NP, NP-Complete, NP-Hard, 시간 복잡도

# 아주 직관적인 설명

P: 폴리노미얼 타임으로 완전한 정답을 구할 수 있는 쉬운 문제

NP: 임의의 값 하나에 대해서만 그것이 정답인지 아닌지 폴리노미얼 타임이하로 계산가능한 검산만 쉬운 문제

보통 NP를 풀때는 휴리스틱 탐색 등의 계산적인 접근법을 사용한다. 

위의 정의에서 P 문제는 애초에 폴리노미얼 타임으로 정답을 구할 수 있으므로, 당연 그 시간내에 검산도 가능하다. 따라서 P ⊂ NP이다.

NP-Hard: NP-Hard는 계산복잡도가 NP일 수도 있고, 그보다 더 어려울 수도 있다. NP-Hard >= NP

영어로는 이렇게 표현한다. "at least as hard as the hardest problems in NP". 그런데 여기서 어렵다의 의미가 조금 복잡하다. 

어떤 NP문제를 다른 문제로 다항식 시간안에 완전히 환원(Reduction)시킬 수 있다면, 그 환원된 문제를 NP-Hard라고 한다.

대충 말하자면 어떤 NP문제의 상위호환격인 문제를 NP-Hard라고 한다. 왜냐하면 NP-Hard가 풀리면, 환원되기 전의 NP문제 역시 같이 풀려버리기 때문이다. 

즉 환원이란 과정은 어떤 문제가 더 큰 문제의 밑으로 들어가는 것을 의미한다. 그래서 더 어렵다라고 표현할 수 있다.

https://wkdtjsgur100.github.io/P-NP/

NP-Complete: NP이면서 동시에 NP-Hard인 문제. NP-Complete = NP ∩ NP-Hard

NP-Complete은 문제의 난이도를 가리키는 말이 아니라, NP문제이면서 동시에 NP-Hard의 성질을 가진 문제들을 가리키는 말이다. 

앞에서 NP-Hard >= NP라고 했는데, 여기서 등식에 해당하는 그 경계선 문제들을 가리킨다고 보면 된다.

즉 어떤 NP를 환원시킨 문제, NP-Hard가 NP시간 안에 풀수 있다는 것이 증명되면 NP-Complete로 승격이 된다.

NP-Complete이 매우 유용한 이유는, 이 문제에 속하는 (NP-Hard로 환원 되기 전의) NP 문제들을 전부 다 이 알고리즘으로 한방에 풀어버릴 수 있기 때문이다.

Polynomial Time:   for some constant  의 계산복잡도를 의미한다.

참고로 '어떤 문제를 다항식 시간 내에 해결할 수 있는가 아닌가'는 '그 문제를 해결하는데 평균적으로 얼마나 시간이 걸리는가?'가 아니라 '최악의 경우(worst case)에 시간이 얼마나 걸리는가?'를 기준으로 한다.

https://namu.wiki/w/P-NP%20%EB%AC%B8%EC%A0%9C#toc

P=NP 인가 혹은 P!=NP 인가?

거의 확실히 P!=NP일 것이다. 왜냐하면 P=NP라는 것은, 그동안 우리가 어렵게 풀수밖에 없었던 모든 문제들이 사실은 너무나 쉬운 문제였다는 말이 된다.

다시 말하면, 어떤 값을 넣어서 이게 정답인지 아닌지 겨우 검산만 가능한 모든 문제들을 이제부터 한방에 정답을 찾을 수 있게 된다는 말이다.

이게 되면 우리는 그 즉시 빛의 속도로 우주를 여행할 것이고, 슈퍼 AI를 만들 것이고, 새로운 차원으로 여행을 떠날 수 있을 것이다.

---

# 클래식한 설명

P : 어떤 문제의 해답을 빠른 시간(다항식 시간)안에 찾을 수 있는 문제.

어떤 문제를 빠른 시간안에 풀 수 있는 알고리즘이 존재한다고 증명되는 순간 그 문제는 P에 속한다.

NP : 어떤 문제에 대해 내가 제시한 답이 정답인지 아닌지만 빠른 시간(다항식 시간)안에 O, X로 판단 할 수 있는 문제.

(따라서 모든 경우의 수를 다 집어넣어봐야한다면, 정답을 찾는 데 매우 오랜 시간이 걸린다.)

이때 만약 어떤 문제가 P라면, 그 문제는 NP에 속한다(집합). 왜냐하면 P라면 빠른 시간안에 정답을 찾을 수 있기 때문에, NP에서 정의한 주어진 값이 정답인지 아닌지 알아내는 것은 너무나 쉽기 때문이다.

NP-Hard : 모든 NP의 instance들을 전부다 빠른 시간(다항식 시간) 안에 이 다른 문제로 환원(Reduction)이 가능할 때.

(Reduction은 문맥상의 의미만 간단히 말하면, A라는 문제를 B라는 문제로 바꾸어서 풀 수 있다는 것이다.)

https://inverse90.tistory.com/entry/PNP-NP-Hard-NP-Complete

NP-Complete : NP이면서 NP-Hard인 문제. 즉 모든 NP 문제들이 이 'NP문제'로 Reduction이 가능할 때.

(어떤 NP 문제가 다항함수 시간안에 NP-Complete으로 Reduction이 가능한 경우, 그 문제도 역시 NP-Complete임이 증명되어있다. 그래서 1개의 NP-Complete이 발견된 이후 많은 문제들이 그 문제를 통해 Reduction 되어 NP-Complete임을 증명했다.)

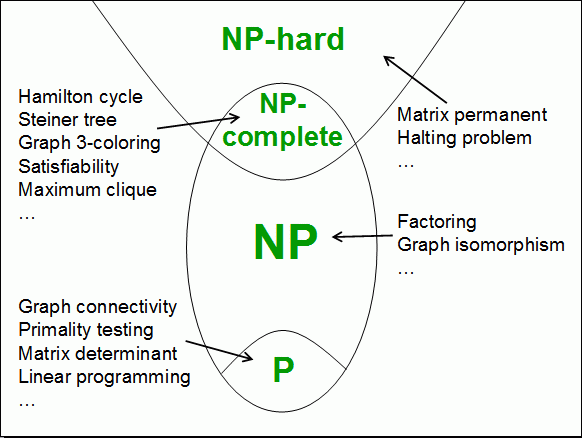
또한 "P이면 NP이다" 는 앞서 본 것 처럼 증명이 되었지만, "NP이면 P이다"라는 명제는 참,거짓이 아직 증명되지 않았다. 아래 그림은 P=NP임이 증명 되었을 때와 P≠NP임이 증명되었을 때의 현상을 잘 나타낸다.

NP=P라면 당연히 NP-Complete 또한 P이므로, 이 말은 수 많은 어려운 문제들을 다항 함수시간안에 풀 수 있다는 것이다. 

마찬가지로 또한 NP-Complete 문제 중 하나를 다항함수 시간안에 풀어낸다는 것은 NP-Complete = P 라는 것이고, 이 역시 Reduction 을 통해 NP=P라는 것과 완전히 동일하다.

현재까지 NP-Complete인 문제 중 다항함수 시간안에 해를 구해내는 알고리즘은 단 하나도 발견되지 않았다. 만약 하나라도 NP-Complete 문제를 다항함수 시간안에 풀 수만 있다면, 모든 NP-Complete을 그 문제로 Reduction 하여 다항함수 시간안에 풀 수 있는 P문제가 되어버린다.

- 시간 복잡도와 Entropy

어떤 문제를 풀기위한 알고리즘의 최소시간 복잡도를 알 수 있을까? 
알 수 있는 문제가 바로 P 이고, 알 수 없는 문제가 바로 NP이다.

(단, 여기서 말하는 시간복잡도는 Worst case에대한 시간복잡도만을 의미한다.)

(시간복잡도에대해 배울때, 사실은 Best case, Average case, Worst case로 시간복잡도를 나타내는 것이 모두 가능하다. 다만 우리는 이 때 Worst case에서의 시간복잡도에 관심이 있는 것이라 일반적으로 시간복잡도라 함은 Worst case를 말하며 이것을 O( f(n) ) 꼴로 나타낸다.)

(http://stunstun.tistory.com/83 참조)

그러면 어떤 알고리즘의 시간복잡도와 entropy는 관련이 있을까?

일단 시간복잡도가 entropy는 아니다.
같은 데이터(정보)를 다룰 때, 다른 알고리즘을 쓰면 entropy는 변하지 않지만 시간복잡도는 알고리즘에 따라 변한다.

ex) 1개의 bit를 반전시키는 알고리즘의 시간 복잡도는 1이다.
ex) 1개의 bit를 3번 반전시키는 알고리즘의 시간 복잡도는 3이다.

즉, entropy와 시간복잡도는 완전히 적용 대상이 다른 개념이라 서로 직접적인 연관성은 없다.
entropy는 데이터가 가진 정보량의 평균값이고, 시간복잡도는 어떤 알고리즘이 수행되는데 걸리는 시간이다.

다만, 어떤 알고리즘에서는 시간복잡도와 entropy가 같을 수 있지만, 이것은 그냥 우연한 하나의 예일 뿐이다.
(bit를 다루는 이진트리의 경우에서 찾을 수 있음.)

http://yoonho.info/19

http://ko.wikipedia.org/wiki/NP-%EC%99%84%EC%A0%84

http://blog.naver.com/gateway21c/167923111