# 유클리드 거리(Euclidean Distance): 유클리드 공간에서의 기하학적 최단 거리(직선 거리)
2차원상에서보면, 두점사이의 직선거리(고차원 상에서도 그릴 수는 없지만, 직선거리 or 최단라고 정의는 가능 할듯.)
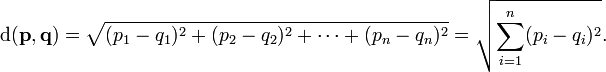
# 마할라노비스 거리(Mahalanobis Distance): 정규분포에서 특정 값 X가 얼마나 평균에서 멀리있는지를 나타내는 거리
관측된 X가 , 얼마나 일어나기 힘든 일인지 즉 평균과 표준편차를 고려했을때 얼마나 중심에서 멀리 떨어져 있는가를 구하는 값. 주로 관측된 데이터의 신뢰성? 또는 적합성을 판단하는데 쓰인다고함.(에러인지를 판단한다)
ex) 평균이 20, 표준편차가 3인 분포에서 26의 데이터가 관측 -> 이때 26의 마할라노비스 거리는 (26-20)^2/3 = 12가 됨. (이 점이 분포에서 얼마나 심하게 떨어졌는가를 수치화한 것.)

두번째 식을보면, 표준정규분포로 바꾸는 과정과 얼핏 유사하다.
http://blog.naver.com/intencelove/20105601093
http://darkpgmr.tistory.com/41
# 맨해튼 거리(Manhattan distance): 격자 형태의 지도에서 한 점에 도달하기 위한 거리
2차원이라면, X끼리뺀 값과 Y끼리 뺀 값들을 전부 합한것(3차원이면 z끼리뺀값을 또 더하겠지)
맨해튼 도시에서 건물 블럭들이 있을때, 몇블럭 이동해야하는지를 측정하는 것에서 유래.


# 민코프스키 거리: p-norm을 활용한 일반화된 거리 공식
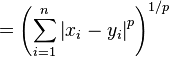
유클리드거리(p=2)와 맨해튼 거리(p=1) 모두 민코프스키 거리에 포함된다.
# 해밍 거리(Hamming distance): 두개의 2진수에서 몇칸이 다른 지 측정 방법이다.
같은 길이를 가진 수열을 비교해서. 몇칸의 데이터가 다른지를 측정
ex) 111000 과 100000의 거리는 2이다(1 두칸이 다름.)
https://en.wikipedia.org/wiki/Hamming_distance
# 레벤슈타인 디스턴스(Levenshtein distance): 두 문자열간의 거리를 재는 방법.
Insertion / Deletiong / Substitution 세가지 방법에 의한 Character의 수정 횟수를 센다.
구체적으로는 Dynamic Programming을 이용해서 두 문자열이 똑같아지기 위한 최소 수정 횟수를 센다.
아래의 라이브러리가 속도가 빠르고 좋다.
https://github.com/roy-ht/editdistance
'Research > Machine Learning' 카테고리의 다른 글
| Clustering, GMM, K-means, EM, DBSCAN (0) | 2014.06.11 |
|---|---|
| Nominal, Ordinal, Interval, Ratio (0) | 2014.06.11 |
| ROC curve, ROC_AUC, PR_AUC, 민감도, 특이도 (15) | 2014.06.11 |
| 조건부 독립과 응용 (0) | 2014.06.06 |
| Overfitting, Underfitting, Cross-validation (0) | 2014.06.06 |

댓글