- Sigmoid 함수 (시그모이드 함수)
대표적인 활성 함수(Activation Function)이다.
뉴럴넷에서 Activation Function 이란, x=Weighted Sum 에대해, y=F(x) 로 output y를 다음 레이어로 보내는 함수 F를 의미한다.
단순히 계단식으로 활성화 함수를 사용할 경우, output이 무조건 0과 1로만 나와, 미분이 불가능하고, 중간 값이 존재하지 않는다.
그러나 시그모이드 함수를 쓸 경우, output을 0과 1만이 아니라 [0,1]의 범위로 feature를 나타낼 수 있다.

여기서 분자분모에 e^x 를 곱하면
로 바꾸어 표현할 수 있다.(두 표현 다 자주 쓰임) 정확히 이런 모양을 가진 함수를 Sigmoid 함수라고 부름.(logistic 함수라고도 부름)
이때 Sigmoid 를 미분하면
S'(x) = S(x){1-S(x)} 가 된다.
(분수를 -1승으로 올린다음 합성함수 미분을 해서 유도하면 됨.)
Sigmoid(5) = 0.99
Sigmoid(-5) = 0.01
- 시그모이드의 역함수 :

http://en.wikipedia.org/wiki/Logit
https://blacklen.wordpress.com/2011/01/01/sigmoid-and-logit-function/
- 여러가지 Activation Function
Sigmoid는 0~1까지로 매핑
(이걸 쓰는 이유는 RBM의 P(X|H)계산식이 Sigmoid라서, 그리고 미분가능해서로 보임)
Tanh(하이퍼볼릭 탄젠트)는 -1~1까지로 매핑. sigmoid의 y축 범위를 2배로 확대한 것. (음수값을 쓰고 싶을 때)
Tanh(x/2) = 2*sigmoid(x) -1 과 완벽히 동치이다.
https://www.wolframalpha.com/input/?i=(2*sigmoid(x)-1)+-+tanh(x%2F2)
Softmax :
소프트맥스는 주로 DNN의 마지막 output Node에서 Classification 을 하고자 할 때 사용된다. 마지막 Layer에서 Softmax로 One of K coding을 함.여러개의 시그모이드값들을 다 더한걸로 각각의 시그모이드값을 나누어 다합치면 1이 되는 확률로써 해석하고자하는 것.
(Softmax에서 평균을 내기위해 전체의 합으로 나누어주는 값을 Z term이라고 한다. 아마도?)
Softmax는 LogisticRegression 을 여러개의 클래스로 extension 내지는 normalization한 것이다.
Softmax : 소프트맥스는 여러개의 시그모이드값들을 다 더한걸로 각각의 시그모이드값을 나누어 다합치면 1이 되는 확률로써 해석하고자하는 것. 주로 DNN에서 output node로 Classification 을 하고자 할 때, 마지막 단계에서 Softmax로 One of K coding을 함.
-
softmax는 logistic regression 을 multiple categorical 변수로 확장시킨 개념이다.
따라서 2개의 변수에 대한 softmax는 logistic regression과 동치이다.
즉 softmax는 k-카테고리칼 변수에 대한 classification에서 어떤 카테고리에 해당할지 확률을 나타내는 데 쓰인다.
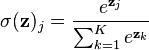 for j=1,...,K.
for j=1,...,K.
위 식에서 K가 2까지 있다면, k=1에대한 softmax는 다음과 같다.

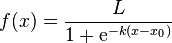 (L이아니라 1이어야함)
(L이아니라 1이어야함)
이처럼 x-x0 값을 즉, x인 경우와 x0인 경우를 뺀 값을 0~1사이의 확률로 표현한다.
- 뉴럴 네트워크에서는 이처럼 x와 w의 내적한 값(weighted sum)에 대해 소프트맥스를 취함

매틀랩 구현 코드
softmax = @(x) exp(x)./repmat(sum(exp(x)')',1,size(x,2));
http://en.wikipedia.org/wiki/Softmax_function
ReLU (Rectified Linear Unit) :
그런데 최근 CNN 연구에서 Activation 으로 Sigmoid가 아니라 y = max(0,x)을 사용하면 더 성능이 좋아진다고 한다.
이것의 수학적인 유도는, 하나의 뉴런으로 들어오는 시그모이드 엑티베이션을 N개를 더한 값이 위 함수와 유사하다는 것이다.
(즉 하나의 input을 N단계의 각도로 살펴보겠다. 여기서의 N단계의 각도는 -1씩 빼는걸 의미함.)
Sigmoid 여러개를 X마다 -1 씩 빼면서 충분히 N단계만큼 더한다. 그러면 결국 N이 커질수록 Sigmoid(X)의 값은 0에 가까워진다.
이때 Log(1+e^x)는 다시 Max 펑션으로 근사할 수 있어서 이 것을 쓴다고 한다.
이 Max 펑션을 쓰게되면, 더욱 표현력이 좋아져서 더 빠르게 학습이 가능하다고 한다.(Minima에 더 빨리 수렴한다.)
(그런데 내 생각엔, 이 걸 쓰게되면 overfitting이 더 심해질 것이라고 보인다.
왜냐하면 x를 무제한으로 받게되면 W가 훨씬 더 빠르게 증가할 것이므로..)
그러나 x를 Sigmoid같은 일종의 억지러 눌러주는 일을 하지 않기 때문에 (ex) Sigmoid(10000000)=Sigmoid(10000) 와 거의 차이가 없음) 오히려 아주 큰 x의 데이터를 잃어버리지 않는 장점이 있다고 보인다.
따라서 ReLU을 쓰되 Regularization을 잘 해주는 것이 더 좋을 수 있다고 본다.
ReLU의 0에 해당하는 부분으로 활성화가 될 경우 이 자체로 Regularizaiton이 강력하게 일어나는 것이라고 한다.
그러나 생물학적인 이해를 기반으로 하면 ReLU는 뉴런의 firing rate를 매우 단순하고 직관적으로 모델링한 함수 일 뿐이다.
또한 미분가능해야한다는 activation function 으로써의 조건이 무시되었지만, 그럼에도 empirical 하게는 아무 문제가 없다. 왜냐하면 미분 불가능한 점에 데이터가 딱 들어갈 확률은 모든 전체 실수값분에 0.00000000000000000000.. 점이 나오는 경우의 수로 0에 가깝기 때문이다. (그냥 리미트 0이라고 해석하여도 무관하다.)
이것을 보완하기 위해 시그모이드를 적분한(불확실함) softplus 라는 함수를 사용할 수도 있긴하다. (미분 불가능한 점 근처에 떨어지는 데이터들이 많을 경우, 성능이 증가할 수 있다.)

(초록색은 softplus , 파란색은 ReLU)
http://en.wikipedia.org/wiki/Rectifier_(neural_networks)
또한 ReLU에서 rectified라는 말은, 교류를 직류로 변환하여 0미만인 전류가 발생하지 않도록 하는 정류에서 유래한 단어이다.
단, RNN계열에서는 ReLU를 적용하지 않는데 이는 RNN에서는 그레디언트 배니싱 또는 익스플로전이 논리니어 펑션때문이 아니라, 리커런트하게 같은 기울기가 계속 곱해지기 때문이라는 것 같다.
그래서 이쪽에서는 현재 시그모이드를 사용하고있다.
- PReLu
- Maxout
'Research > Deep Learning & Application' 카테고리의 다른 글
| CNN, Spectrogram 을 CNN으로 학습 (0) | 2015.04.22 |
|---|---|
| TDNN, RNN, LSTM, ESN (0) | 2015.04.15 |
| RNN 학습 알고리즘, BPTT (2) | 2014.07.08 |
| Perceptron, TLU (0) | 2014.06.17 |
| Neural Network의 학습 방법, Gradient Descent, Back-Propagation (2) | 2014.06.17 |





댓글