# 컨퓨전 매트릭스
- True/False: 모델이 잘 맞췄느냐 못맞췄느냐를 의미함. 즉 True이면 모델이 정답을 맞췄다는 의미이고, False이면 모델이 정답을 틀렸다는 의미이다.
- Positive/Negative: 모델이 예측한 값이 True였나, False였나를 의미함.
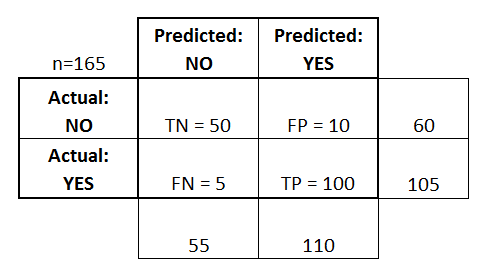
http://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/
- TP: 정답을 맞췄고(T), 모델이 1이라고 예측(P)함. 즉, 실제 정답도 1임
- TN: 정답을 맞췄고(T), 모델이 0이라고 예측(N)함. 즉, 실제 정답은 0임
- FP: 정답을 틀렸고(F), 모델이 1이라고 예측(P)함. 즉, 실제 정답은 0임
- FN: 정답을 틀렸고(F), 모델이 0이라고 예측(N)함. 즉, 실제 정답은 1임
- Precision = TP / TP+FP
-> 내가 맞다고 내린 결정이 진짜로 정답일 확률
-> 모델이 1이라고 예측한 것들 중, 실제로 정답도 1인 것
(1에 가까울수록 좋다. 모델이 정답이라고 추측 한 것이 과연 얼마나 믿을만한지를 측정함=신중한 판단)
ex) 판사가 어떤 범죄자의 무기징역을 결정할 때, 절대로 무고한 사람이 형을 살지 않도록 아주 신중하게 결정해야한다.
- Recall = TP / TP+FN
-> 놓치지 않을 확률
-> 실제 정답이 1인 것들 중, 모델이 1이라고 예측한 것
-> 전체 전염병환자들 중에서, 내가 놓치지 않고 잡아낸(소환해낸) 비율
(1에 가까울수록 좋다. 모델이 정답을 얼마나 놓치지 않고 다 잡아오는가(Recall)를 측정함=놓치지 말것)
ex) 의사가 전염성이 아주 높은 병의 격리 여부를 결정할 때, 절대 전염병 환자를 놓치지 않기 위해서는 조금이라도 의심이 가면 격리를 시켜야한다.
- Accuracy = TP + TN / TP+TN+FP+FN
-> 전체 경우들 중에서, 모델이 제대로 정답을 맞춘 비율
(1에 가까울수록 좋다. 모델의 종합 성적)
- Average Precision: Precision-Recall curve에서 밑면적의 넓이를 계산한 것.
* 주의: AUC와 개념적으로 거의 동일하고, 다만 차이점은 x축과 y축이 조금 다를 뿐임.
마찬가지로 threshold를 바꿈에 따라 변하는 Precision과 Recall의 값을 그래프로 그리고, 이것의 밑넓이를 적분해서 구한것이다.
- Mean Average Precision: AP를 모든 class에 대해서 계산한다음, 그것을 전체 평균낸 것.
https://stats.stackexchange.com/questions/260430/average-precision-in-object-detection
http://darkpgmr.tistory.com/162
https://en.wikipedia.org/wiki/Information_retrieval#Mean_average_precision
https://www.kaggle.com/wiki/MeanAveragePrecision
http://enginius.tistory.com/374
# Multi-label Confusion Matrix
일반적인 multi-class confusion matrix 계산과 달리, multi-label task에서는 confusion matrix가 3차원형태로 계산되어진다.
2차원 사용이 불가능한 원인 :
ex. label이 [1,3], 예측이 [1,4]라면, 두가지 할당 방법이 존재,
a. Confusion-Matrix에서 [1, 1], [3,4]에 데이터를 할당하는 방식
b. Confusion-Matrix에서 [1, 1], [1,4], [3,1], [3,4]에 데이터를 할당하는 방식
a. 방법의 예외 상황
(ex) label이 [1,3, 4], 예측이 [1,4]라면,
Confusion-Matrix에서 [1, 1], [4,4] 할당 후에 [3]은 어떤 식으로 할당이 되어야 하는지?
(ex2) label이 [1, 3, 4], 예측이 [1, 4, 5, 6]라면,
Confusion-Matrix에서 [1, 1], [4,4] 할당 후에 [3,5], [3,6] 중에서 누구로 할당이 되어야 하는지?
b. 방법의 예외 상황
(ex )label이 [1, 4], 예측이 [1,4]라면
[1,1], [1,4], [4,1], [4,5]와 같이 할당이 가능한데, [1,4], [4,1]라는 오류를 같이 할당해야하는 문제
https://scikit-learn.org/stable/modules/generated/sklearn.metrics.multilabel_confusion_matrix.html
'Research > Machine Learning' 카테고리의 다른 글
| Thompson Sampling, Multi-armed bandit, Contextual bandit (0) | 2018.01.05 |
|---|---|
| Natural Language Processing (0) | 2017.08.14 |
| Coefficient of Determination(결정계수), R^2(R square) (0) | 2017.05.22 |
| Decision Tree 계열 알고리즘 (0) | 2017.02.13 |
| On-policy와 Off-policy, Policy Gradient, Importance Sampling (0) | 2017.01.03 |



댓글