표본평균의 평균
표본평균이 모평균과 같은게 아니라, 표본평균의 평균이 모평균과 같다.
가장 크게 착각하는 점이 모집단에서 임의로 N개의 샘플을 뽑은 단 1개의 표본집단의 평균은 절대 모평균과 같지 않다.
고등학교 확률에서 말하는 개념은, 이러한 N개 샘플을 뽑은 표본집단이 충분히 큰 수인 M개가 있을 때, 각각의 표본집단을 평균내서 만든 표본평균들의 평균이 모평균과 같아진다는 말이다. 이 경우 표본평균들의 분산이 모집단의 분산보다 작은 이유는 쉽게 납득 가능하다. 당연히 표본평균들은 이미 1차적으로 표본집단에 대해서 평균이 취해지는 과정에서 분산이 상당히 사라지기 때문이다.
즉, 이 표본평균이라는 확률변수는 아래와 같은 분포를 따른다.
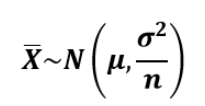
즉, 이 "표본평균"이라는 녀석은 표본집단을 평균 냈을 때의 변수이고, 이 변수는 위와 같은 정규분포로부터 샘플링이 되는 것이다. 정규분포를 따르는 이유는 중심극한의정리에 의해, 모집단이 어떤 분포이든 상관없이 표본평균에 대한 분포는 정규분포이기 때문이다. 위의 수식에서 가장 중요한 것은 표본평균이라는 변수가 (모평균의 분산/N)의 분산을 갖는 다는 것이다. 이 개념을 통해서 우리는 추후 단 1개의 표본집단을 통해 구한 표본평균을 통해 모집단의 평균을 추론하는 신뢰구간을 유도해내게 된다.
표본의 분산
표본의 분산은 방금 위에서 살펴본, 표본평균들의 분산과 다른 개념이다. 표본의 분산은 모집단에서 N개의 샘플을 뽑아서 단 1개의 표본집단을 만들고, 이 표본집단에 대해서 분산을 계산한 것이다. (위에서 나온 표본평균의 분산은, 표본집단을 M개 만들고, 각각을 평균을 냈을 때, 그 표본평균들이 따르는 분산을 의미한다.) 그래서 이 표본집단에 대해서 분산을 구할때는 N이 아니라, N-1로 나누어야 한다.
표본의 분산을 구할 때 N이 아닌 N-1로 나누는 이유는 다음에서 매우 직관적으로 설명되어 있다. 수학적인 정확한 이유는 자유도가 N-1이기 때문에, unbiased esitimation을 하기 위해서는 N-1로 나눠줘야한다.
표본분산을 구할때 n-1로 나누는 이유를 질문하신게 맞지요?
모집단의 분산을 구할때는 n으로 나눠주지만,
표본분산을 구할때는 자유도로 나눠줍니다. 자유도란 말그대로
자유롭게 값을 가질수 있는 수인데요~예를들어서 설명해 드리겠습니다.
A, B, C 세 사람이 있습니다.
세 사람의 키의 평균은 180이라는 것을 알고 있습니다.
그리고 A의 키는 170, B의 키는 190이라는 것을 알고있다면
C의 키는 몇일까요?평균이 180이었으므로 당연 180이 되겠지요?
이렇게 평균의 값을 알고있게 됨으로써 C의 키는 180으로 고정됩니다.
다시말해 A와 B의 키가 어떻게 되든지 그 값만 알고 있다면 C의 키는 자연스럽게
알게 됩니다.
위의 경우에서 평균을 알고 있으므로 두명은 자유로운 값의 키를 가질수 있지만 한명은
그 두명에 의해서 키가 고정되버려 자유로운 값을 가질 수 없지요?
따라서 자유도는 (n-1)=3-1=2 가 됩니다.
다시 표본분산으로 돌아오면,
표본분산을 구하기 위해서는 평균을 알아야하겠지요?
따라서 평균을 알고있는 상태이기 때문에 자유롭게 가질수 있는 값은
n-1이 되버린겁니다~
-
정리하자면, 표본의 분산을 구하기 위해서는 먼저 표본의 평균을 구해야만 한다.
그런데 평균을 구하게 되면, 임의의 데이터 하나는 나머지 데이터의 값들과 아까 구한 평균에 의해 그 값이 고정되어 버린다.
즉 어떤 데이터 1개는 평균을 구하면서 값이 고정되어, 분산을 가질 수 없다는 것이다.(=얘는 자유도가 없다.)
그러므로 표본의 분산을 구할 때는 이 데이터를 뺀 N-1로 나누어야 한다.
이러한 현상을 bias 되었다고 한다. 물론 이것은 표본의 크기 N이 충분히 크면 별 문제 없으나, 표본은 보통 모집단에 비해 굉장히 작은 크기로 사용된다. 그러므로 보통 N-1로 나누어 주면 좀 더 정확하다.
모평균의 추정에 대한 비판
사실 위에서 언급된 표본평균의 평균이나 분산과 표본의 분산은 실용적으로 그다지 쓸모가 있는 개념은 아니다. 왜냐하면 표본집단을 무수히 많이 뽑아야 모평균을 추정할 수 있다는 얘기는 무수히 많은 돈을 들어야 모평균을 추정할 수 있다는 얘기와 같기 때문이다.
실제 우리 생활에서 중요한 개념은 단 1개의 표본집단으로부터 모평균의 평균을 추정하는 것이다. 이때 사용되는 개념이 바로 신뢰구간이다. 이에 대한 자세한 개념과 과정은 링크된 블로그를 참조하기 바란다.
다만 여기서 내가 강조하고 싶은 포인트는 통계학에서 모평균을 추정하는 방법이 얼마나 강력한 가정을 필요로하는지만 말하고 싶다.
우선 모평균은 모르지만, 모표준편차를 알고 있고, 모집단이 정규분포를 따른다는 걸 알고있다는 것은 엄청난 가정이다. 일단 모집단이 정규분포일 것이다라는 가정까지는 경우에 따라 합리적일 수 있다. 예를 들어 측정하고자 하는 변수가 남성의 키와 같이 정규분포라고 자연히 가정할 수 있는 경우가 있다. 그러나 만약 남성의 키가 아니라, 성별을 알 수 없는 그냥 사람의 키는 정규분포일까? 아니다. 2개의 정규분포가 합쳐진 bi-modal 분포이다. 즉 정규분포라는 가정이 성립될 것이라고 합리적으로 추론할 수 있을 때만 가능하단 말이다.
그리고 이 정규분포의 표준편차는 아는데 평균은 모른다? 사실 이거는 현실에서는 99% 불가능하다. 왜냐하면 표준편차(혹은 분산)을 구할 때 평균의 개념이 사용되기 때문이다. (X^2의 평균 - 평균^2 or 편차^의 평균) 그래서 사실 이 개념이 유용하기 위해서는 모집단이 정규분포라고 합리적으로 가정할 수 있고, 모집단의 표준편차에 대해서도 사람이 임의의 가정을 넣을 수 있을 경우에만 유효하다.
그다음으로 모평균도 모르고, 모표준편차도 모를때 t분포를 사용하고, 모표준편차 대신 표본의 표준편차를 사용하면된다는 것 또한 상당히 비현실적이다. 일단 모분산을 모르기 때문에 표본집단에서 구한 표본분산을 사용하는 것까진 어쩔수 없는 합리적인 선택이지만, T분포를 가정하면 해결된다는 것은 역시나 실제 현실과 동떨어진 가정이다. T분포와 정규분포의 차이점은 오직 표본의 수가 적을 때 t분포가 바깥쪽 확률(outlier)에 대해서 좀 더 높은 가정치를 주었다는 것밖에는 없다. 즉 정규분포를 가정한거나 T분포를 가정한 것이나 현실과의 괴리에 대한 위험성은 별반 다르지 않다.
그래서 결론은?
기계학습에서는 어떠한 모분포를 추정하기 위해서, learnable parameter로 표현된 임의의 확률모델을 Maximum Likelihood Estimation(MLE)으로 fitting하는 방법이 가장 많이 사용한다. 즉 이 또한 모집단이 어떤 분포를 따를 것인지에 대해서 사람이 매우 강력한 가정을 집어넣고서, 매우 많은 데이터(표본)로 계산을 해야만, 실제 분포와 가까운 모델링이 가능하다는 것이다. 즉 모분포에 대한 추정은 매우 매우 어렵다는 얘기이다. (사실은 신뢰구간 역시, 정규분포와 표준편차를 가정한 확률모델을 MLE로 학습한 것이라고도 말할 수 있다.)
다만 그렇다면, 위와 같이 정규분포와 T분포를 이용한 신뢰구간 추정은 쓸모가 없느냐? 그렇지는 않다. 우리가 논리적이고 확률적인 사고를 하기 위해서는 (ex. A/B test에서 최소 샘플 수 선정) 다소 거칠고 투박하더라도 모집단에 대한 정규분포 및 표준편차를 가정해서 사고를 해야할 필요성이 있기 때문이다. 그러나 이 방법은 진짜 말그대로 사고를 하기 위한 도구이지, 이것이 절대적으로 옳다고 생각해선 안될 것이다.
'Research > Science & Mathmatics' 카테고리의 다른 글
| 3대 작도 문제 (0) | 2015.04.02 |
|---|---|
| 뇌과학 - Place cell (0) | 2015.03.03 |
| 확률 법칙, The Rules of Probability. (0) | 2014.08.11 |
| Jacobian Matrix, Fisher Matrix, Hessian Matrix, (0) | 2014.08.06 |
| [NeuroScience] New born neurons (0) | 2014.07.22 |


댓글