본문 바로가기
A. Research/Machine Learning

Advanced Gradient Descent Method

by IMCOMKING 2015. 10. 24.

Advanced Gradient Descent Method (고급 경사 하강 법)

출처 : http://imgur.com/a/Hqolp

위에서 소개된 그림은 특정한 landscape에서의 각각의 optimizer들의 학습 속도를 표현 한 것이다. 보기에는 Adadelta가 최고인가하고 생각 할 수 있겠지만, 문제 상황에 따라 잘하는 경우도 있고, 못하는 경우도 있으므로 문제 상황에 맞게 잘 선택해야한다.


출처 : http://imgur.com/a/Hqolp

위의 이미지는 특히 Rmsprop와 Adagrad가 좋은 성능을 보인다. 뉴럴넷의 W와 같은 고차원의 공간에서는 이러한 saddle point가 매우 많아 문제가 되는 것으로 알려져있다. 따라서 이 두가지 옵티마이저를 선택하는 것은 좋은 방법이다. 

요즘에는 Adam이라는 optimizer가 기본으로 쓰는 경우가 많고, 경우에 따라 non-stationary가 심한 문제(강화학습 등)에서 RMSprop를 선택하는 경우가 많다.


-


GD (Gradient Descent): GD는 가장 기본적은 뉴럴넷의 학습 방법으로, 전체 데이터에 대한 Error함수를 Weight로 미분하여 계산한 각 W 파라미터에 대한 gradient를 이용하여 Weight를 업데이트한다. 이 때 얼만큼의 gradient를 사용할지 결정하는 값을 learning rate라고 하는데, 이 값에 따라 local minima에 빠지거나 발산하는 경우가 있다. 또한 전체 데이터에 대한 계산을 한 뒤에 W를 업데이트하기 때문에, 계산량이 너무커 W가 optimal을 찾아가는 속도가 느려 현재는 거의 쓰이지 않고 있다. Batch Learning이라고도 부른다. 또한 gradient descent는 기울기가 양수(+)이면 w를 음수(-)방향으로 이동시켜야 하므로, 기울기의 반대 부호로 움직인다고 볼 수 있다.

W' = W − λ f'(W)     ( λ 는 learning rate이다.)


SGD (Stochastic Gradeint Descent): SGD는 위에서 GD가 갖는 너무 큰 계산량 문제를 해결하기 위해 전체 데이터중에서 랜덤하게 추출한 1/N의 데이터만을 사용해 훨씬 더 빠르게, 자주 업데이트하는 방법이다. 이 때 추출한 1/N의 데이터를 Minibatch라고 부르며, 이 데이터가 전체 데이터의 분포를 따라야만 제대로 된 학습이 가능하다. 만약 이 데이터가 전체 데이터의 분포를 따르지 않고, 계속 분포가 바뀌는 non-stationary한 경우를 online learning이라고도 부른다.

전체 데이터를 잘 섞어서, 너무 작지 않은 크기로 N 등분하면, 계산량이 1/N 배가되어, 빠르게 Weight를 업데이트할 수 있어, 이론상 N배 더 빠른 학습이 가능하다.

추후 SGD에서 각 Minibatch 분포가 매번 약간씩 달라지는 noise를 internal covariate shift라고 부르며, 이를 해결하기 위한 방법으로 batch-normalization이 등장한다.


Downpour SGD: Downpour SGD는 DistBelif라는 구글의 모델, 데이터 병렬화 학습 모델에서 소개된 방법이다. 간단히 말하면 여러개로 모델을 쪼개어, 여러개의 머신에서 동시에 학습을 하는데 이 때 여러 모델들에서 계산된 gradient를 평균내서 각각의 모델에 적용하는 방법이다. 이렇게 해도 충분히 전체 데이터와 모델에 대한 근사적인 학습이 가능하다고 하다.

http://static.googleusercontent.com/media/research.google.com/ko//archive/large_deep_networks_nips2012.pdf


Per-dimension learning rate: 이 원리는 Momentum 및 기타 여러 advanced optimizer들의 핵심을 관통하는 개념이다. 짧게 설명하자면 각각의 차원마다 서로 다른 learning rate를 사용해야만 더 빠르게 saddle point를 벗어날 수 있다는 것이다. 예를 saddle point에서 long narrow valley 방향으로의 gradient값은 매우 작지만, 이쪽 방향으로 빨리, 많이 학습해야만 이 saddle point를 벗어날 수가 있다. 따라서 이쪽 방향으로의 learning rate는 커야한다. 이러한 개념은 아래 소개되는 advanced method에서 공통적으로 통하는 개념이다.

자세한 내용은 아래 글 참고하기 바란다.


The heuristic annealing procedure discussed above modifies a single global learning rate that applies to all dimensions of the parameters. Since each dimension of the parameter vector can relate to the overall cost in completely different ways, a per-dimension learning rate that can compensate for these differences is often advantageous. When gradient descent nears a minima in the cost surface, the parameter values can oscillate back and forth around the minima. One method to prevent this is to slow down the parameter updates by decreasing the learning rate. This can be done manually when the validation accuracy appears to plateau. This gives a nice intuitive improvement over SGD when optimizing difficult cost surfaces such as a long narrow valley. The gradients along the valley, despite being much smaller than the gradients across the valley, are typically in the same direction and thus the momentum term accumulates to speed up progress. In SGD the progress along the valley would be slow since the gradient magnitude is small and the fixed global learning rate shared by all dimensions cannot speed up progress. These oscillations are mitigated when using momentum because the sign of the gradient changes and thus the momentum term damps down these updates to slow progress across the valley.



Momentum: 모멘텀은 저렴한 2차 최적화방법(cheap second order optimizer)라고도 불리우는 방법으로 구현과 원리가 매우 간단하면서 어느정도 좋은 성능을 내는 것으로 알려져 있다. 원리는 sgd에서 새로 계산된 gradient를 바로 사용하는 대신, 한 스텝 전의 gradient를 일정한 %만큼 반영하여 새로 계산된 gradient와 합해서 사용하는 것이다. 즉 원래의 gradient를 일정 부분 유지하면서 새로운 gradient를 적용하여, 관성 모멘트같은 효과(속도가 존재)를 주는 방식이다. 이를 통해 local minima를 더 빨리 빠져나올 수 있다. 그리고 결국 이 모멘텀에는 과거의 모든 gradient가 계속해서 일정한 %씩 누적되어 있게 된다.

V = µV' + λ f'(W)     ( µ는 모멘텀을 얼마나 반영할지 결정하는 상수이다.)
W' = W - V

단 이때, 러닝레이트가 너무 크면 weight가 발산해버릴 수 있으므로 작게 설정해야 한다.
ex) SGD(lr=0.1, decay=1e-6, momentum=0.9, nesterov=True) # VGG에서 사용한 모멘텀




NAG (Nesterov’s Accelerated Gradient Descent): 모멘텀에서 한 단계 더 발전된 방법으로 다음과 같은 수식을 통해 W 업데이트가 이루어진다.

V = µV' − λ f'(W + µV)
W' = W - V

즉 현재의 W에서의 gradient를 계산하기 전에, 먼저 학습했던 V만큼 한 번 더 가본 상태(W+µV)에서 gradient를 계산하는 것이다. 이것은 예를 들자면, 관성에 좀 더 힘을 주어 일단 먼저 갔던 속도만큼 가본다음에, gradient를 계산해서 방향을 조정하겠다는 것이다. 결국 보다 공격적으로 속도벡터 V를 활용하겠다는 것이다. 나머지는 모멘텀처럼 그전 V를 일정부분 반영해서 업데이트를 한다. 아래의 그림과 논문을 보면 좀더 직관적인 이해가 가능하다.

Adagrad:

Adagrad는 러닝레이트를 다음과 같은 노멀라이제이션 L2 term으로 나누어주는 것이다.



Adadelta: Adagrad의 문제를 해결하겠다고 등장한 연구이나 실제로는 Adagrad가 더 잘하는 경우가 많다. 다음 글을 참조.





RMSProp: Non-stationary 한 데이터를 학습시킬 때 많이 사용한다.


http://sifter.org/~simon/journal/20150415.html

http://climin.readthedocs.org/en/latest/rmsprop.html#tieleman2012rmsprop

http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf


RMSProp with momentum: 


Adam: 최근의 딥러닝에서 가장 많이 default로 사용되는 optimizer이다.

The method combines the advantages of two recently popular optimization methods: the ability of AdaGrad to deal with sparse gradients, and the ability of RMSProp to deal with non-stationary objectives.

http://arxiv.org/pdf/1412.6980v8.pdf


-


Learning Rate Decay : 위에서 살펴본 여러 optimizer들 또한 어느정도 learning rate의 스케일을 조절하는 기능은 있다. 그러나 practical 한 관찰 결과 이들의 기능은 각 dimension 마다 움직여야할 학습률의 비율을 찾아주는 효과가 강하다. 그래서 scaling을 따로 해주는 기능을 추가로 구현하는 것이 더 성능을 좋게할 때가 많다.

간단한 예를 들자면, 아래와 같은 Loss - Weight space에서는 0.1의 learning rate로 학습을해서 점점 더 낮은 지역을 찾아가는데, 문제는 이를 충분히 학습시킨 Loss - Weight space역시 아래의 모양과 동일하게 울퉁불퉁한 landscape을 가지고 있다는 점이다. 즉 마치 프랙탈 처럼, 충분히 학습을 해서 space를 더 좁은 공간으로 파고 들어도 마찬가지로 동일한 모양의 space가 나온다는 것이다. 그러면 당연히 학습을 할수록 learning rate의 크기는 확대된 공간 만큼 줄어들어야 할 것이다. 이러한 이유 때문에 learning rate decay가 필요하다.

stochastic gradient descent에 대한 이미지 검색결과

그러므로 Adam을 사용함과 동시에 특정한 스텝마다 learning rate를 1/2씩 exponential하게 줄여주는 기능을 같이 사용하는게 더 좋은 성능을 보인다.

그러나 언제 learning rate decay를 해야할지 결정하는 것은 굉장히 어렵다. 단순히 일정 iteration마다 decay를 하게되면 문제마다 그 iteration길이를 조정하는 것이 다르기 때문에 쓰기가 매우 힘들다. 그래서 가장 무난 방법은 Loss가 더이상 감소하지 않고 장시간 수렴해버리거나, 오히려 Loss가 일정시간 증가하는 것이 관찰될 때 learning rate decay를 해주는 것이 좋아 보인다.


Weight decay :

Weight의 크기에 비례하여, weight 업데이트속도를 더 낮추는 regularizer. L2 regularization과 특정한 조건에서 동치일 수 있다.

https://stats.stackexchange.com/questions/29130/difference-between-neural-net-weight-decay-and-learning-rate


Conjugate Gradient: 일단 간단히 설명하자면 보다 수학적으로 과거의 gradient를 고려하여 현재의 gradient를 계산하겠다는 것이다. 모멘텀이나 NAG는 보다 naive하게, 과거의 속도를 그냥 일정한 %만큼 남겨두는 방식이지만 conjugate gradient는 positive semi-definite을 이용하여 새로운 gradient가 과거 gradient와 conjugacy을 만족하도록 계산한다.

V = βV' − λ f'(W')
W = W' - V
β = f'(W')^t * A * V' / V'^t A V 
(V^t 는 V의 transpose를 의미한다. A는 2차함수의 행렬에 해당하며 symmetric이라는 가정이 있다.)

이때 β를 계산하는 것이 conjugate gradient의 핵심인데, 이는 V^tAV'=0 라는 conjugacy의 정의를 통해 구해진다. 사실 conjugate gradient는 2차원의 quadratic 형태로 테일러 근사시킨 함수에서 gradient=0이 되는 지점을 찾는 뉴턴메서드에서 발전한 것이다. 즉 뉴턴메서드에서 W를 업데이트하는 V를 정할 때, 과거의 V'와의 conjugacy를 고려하면서 찾겠다는 것이다.
따라서 이를 만약에 (테일러 근사 없이) nonlinear 함수에서도 적용하기 위해서는 몇가지의 일반화가 적용된 β가 필요하다.(링크 참조)



Natural Gradient: Loss를 minimize하는 gradient를 그냥 단순히 업데이트한다고 해서, 업데이트 된 분포가 과연 더 나은 distribution이 분포인가에 대한 의문에서 출발함.

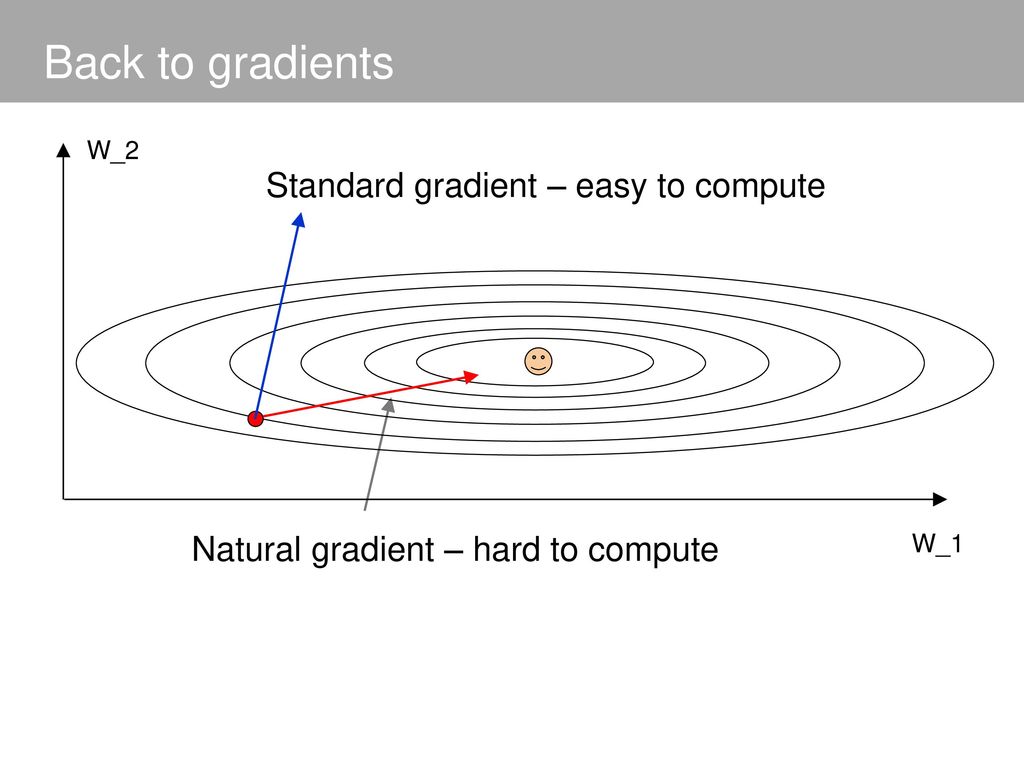
즉 "확률 분포"를 좋게 만드는게 목표인데, 그걸 단순히 Loss값에 대한 미분으로 얻은 gradient를 업데이트한다고 해서 정말로 좋은 분포가 될 것인가(물론 Loss는 줄어들 겠지만..) 

일반적인 sgd를 사용할 경우 미니배치 샘플에 따라 매우 불안정한 학습과정을 거칠 수 있기 때문에 더욱이 문제가 됨. 그래서 natural gradient를 사용하여 분포가 안정적으로 수렴할 수 있게 해줌. 

특히 이런 문제는 RL에서 policy gradient를 구할 때 outlier sample이 등장하는 경우, 매우 안좋은 policy가 생김으로써 학습이 불안정해질 수 있음. 그래서 TRPO에서는 natural gradient를 사용한것으로보임.


* 보다 구체적인 설명: SGD를 이용해서 각 dimension에 대한 gradient를 구할 경우, 일관된 learning rate로 모든 dimension에 대해서 small distance만큼 업데이트를 하게 된다. 그러나 이렇게 업데이트하는 것보다는 각 dim이 local minima로 가는데 필요한 만큼을 정확히 계산해서 update하는 것이 훨씬 빠른 수렴을 가능하게 할 것이다. 이러한 per dimensional learning rate 를 KL divergence를 기반으로 두 분포의 차이가 최소화가 되는 방향으로 constraint를 갖고서 계산하는 것이 natural gradient 이다.
natural gradient descent에 대한 이미지 검색결과


Line Search(Root-finding) : 라인서치는 기본적으로 함수에서 y=0이되는 지점을 iteratvie한 방법으로 찾아가는 것이다. secant method는 서로 y값의 부호가 다른 x1과 x2을 선택한다음, 두 점사이의 직선을 긋고, 그 직선의 y값이 0이 되는 지점을 새로운 x3로 탐색해 보는 것이다(즉 함수를 선형으로 가정하고 탐색하는 것). bisection method는 마찬가지로 서로 부호가 다른 x1과 x2 을 정한다음, 두 점의 평균값을 x3로 선택한다. 그 다음 f(x1), f(x2), f(x3)의 부호를 비교해서 부호가 바뀌는 두 점을 다시 선택해서 위를 반복하는 binary search 알고리즘이다(계속해서 탐색 공간을 반씩 줄여나감). 아래에서 소개되는 뉴턴메서드도 결국 미분한 값이 0이 되는 점을 찾는 일종의 라인서치 방법 중 하나이다.



Newton's Method: 뉴턴메서드는 sgd보다 한단계 더 발전된 gradient descent 방법이다. 현재의 w'점 근처에서의 Error 함수를 테일러 급수 2차미분까지 사용해서 근사한다. 그렇게 근사한 에러 함수는 다음과 같다. (여기서의 w는 1차원이다.)
f(w+w')=f(w') + f'(w')w + f''(w')w^2/2
이때 이렇게 w'근처에서 근사된 함수를 최소화하기위해서는 위의 식을 미분해서 값이 0이되는 점을 찾으면 된다. 이를 정리하면 다음과 같다.
f(w')+f''(w')w = 0 이므로, w = -f'(w')/f''(w')
이러한 아이디어를 활용하여 gradient를 업데이트 하는 방법이다. 업데이트는 결국 다음과 같은 식으로 이루어진다.

V = f'(w) / f''(w)      (다차원 w에서는 V = inv(H) * f'(W) 으로 표현 된다.)
w' = w - λ V

(결국 최종 수식은 마치 learning rate에 1/f''(w)를 곱해주는 것과 같은 식이다. 사실 이러한 원리가 Adagrad, Adam이 개발되게 된 배경이다.)

뉴턴메서드는 에러 함수에 대한 2차 테일러 근사가 좋고, 에러 함수가 w' 근처에서 quadratic하다면, w' 근처의 local minima를 한 번에 찾을 수 있다는 아이디어이다. 이는 곡률이 작은 즉, 완만한 형태의 에러 함수에서는 굉장히 빠른 속도로 학습을 할 수 있고, 반대로 곡률이 큰 곳에서는 

# 궁금증 : 가정상 에러함수 f는 미분이 가능해야 할것이다. 뉴럴넷의 에러함수는 미분이 가능하고, 2차미분 또한 가능하다. 그리고 테일러 급수로 근사된 함수를 미분해서 이것이 0이 되는 점이 최소값이라는 것도 맞는 말이다. 그런데 궁금한 것은 w=F(w')의 형태의 closed form이 존재하지 않으면 어떻게 하지? 뉴럴 넷은 W에 대한 클로즈드 폼이 존재하지 않는데도 이러한 가정이 성립할 수 있는가? 아니면 그냥 적당히 클로즈드 폼이 없어도 2차함수에 근사할 경우 동작한다는 아이디어를 기반으로 적용하는 것인가?




Hessian Free: 먼저 Hessian이란, 어떤 함수를 벡터로 두번 미분해서 계산한 결과 행렬을 의미한다.(즉 자코비안을 한 번 더 미분한 것이다.) 즉 헤시안은 위에서 설명한 뉴턴메서드를 다차원 W 벡터에 적용하기 위해서 필요한 것으로, f''에 해당하는 것이 바로 헤시안이다. 이 헤시안을 이용해 위의 뉴턴메서드를 다차원의 W에 대해 적용해보자.
W = W' -inv(H(W')) f'(W')    ( W의 gradient에 H의 역행렬을 곱해준다.)
뉴턴메서드에서 f''으로 나누는 것이 헤시안의 역행렬을 구하는 것과 같기 때문에, 위와 같은 식이된다.

그런데 이 헤시안의 역행렬을 구하는 것에서 다음 두가지 큰 문제가 발생한다. 먼저 n차원 W에 대한 헤시안 계산은 O(n^2)의 매우 큰 계산량을 요구한다. 두번째 문제는 심지어 딥 뉴럴 네트워크에서 헤시안을 계산하는 방법을 전혀 모른다는 것이다.

# 왜 헤시안을 뉴럴넷에서 계산하는게 어려울까? 단순히 2층의 뉴럴 넷(logistic regression)이라면 충분히 가능할 것 같긴하다. 그런데 3층 이상의 deep구조에서는 먼저 backpropgagtion을 이용해서 에러 함수를 W들로 한번 미분한 다음, 그것을 다시 전체 W로해서 한 번 더 미분해야한다. 이 때 아래층에서 계산한 W'을 위층의 W로 미분하려면 뭔가 전혀 새로운 연구가 필요해 보인다.

이러한 문제들을 해결하기 위해 등장한 것이 바로 Hessian Free Optimization이다.

일단 간단히 설명하자면 헤시안 행렬 H를 직접 계산하지 않고, Hw를 계산해서 쉽고 빠르게 쓰겠다는 것이다. 
먼저 뉴턴메서드에서 테일러 급수로 근사한 2차 함수는 다음과 같다.
f(w+w')=f(w') + f'(w')w + w^t Hw
즉 이러한 2차 함수에서 conjugate gradient를 수행할 경우, H는 항상 Hw를 이용해서 간접적으로 사용될 수 가 있다. Hw는 H보다 훨씬 계산이 간편하기 때문에 계산량 문제는 해결되었다. 또한 일반 backpropagation과 유사한 방식으로 뉴럴네트워크에도 적용이 가능하다.



Positive Hessian: 그러나 위에서 구한 헤시안은 한가지 문제점이 있다. 바로 positive-semi definite이라는 조건이 만족하지 않을 수도 있다는 것이다. 이것이 만족되지 않을 경우 에러가 오히려 높아지는 역방향으로 학습이 일어날 수가 있다. 그래서 제시되는 해결책 첫번 째는, 그냥 음수의 eigen value를 양수로 바꿔서 쓰면 된다는 것이다. 그렇게 eigen value에 절대값을 취해 그냥 부호만 바꾸어서 사용해도 아무런 문제가 없다는 것이 증명되었다.


Gauss-Newton Matrix: 위에서의 문제를 해결하는 또다른 방법은 헤시안을 가우스-뉴턴 메트릭스로 근사해서 사용하는 방법이다.
H = J^t * J  (J 는 뉴럴 네트워크의 자코비안 행렬이다.)
이렇게 정의된 H는 항상 positive-semi definite을 만족하기 때문에, 역방향으로 일어나는 학습이 사라지게 된다.



Quasi-Newton Method: 이것역시 헤시안 프리 옵티마이제이션 처럼, 헤시안을 직접 계산하지 않고, 연속된 gradient 벡터를 통해 근사적으로 계산하는 방법이다. 이는 scent method를 일반화한 개념이며, 이것 말고도 헤시안을 근사하는 방법이 굉장히 많은듯 하다.




- 그 이외 최신 구현되어 유행을 타는 optimizer를 아래에서 확인할 수 있다.

http://keras.io/optimizers/

- 다음 블로그에 매우 좋은 내용이 잘 정리됨!
http://sebastianruder.com/optimizing-gradient-descent/

,

'A. Research > Machine Learning' 카테고리의 다른 글

PPL 원리와 구현  (0) 2022.05.16

관련글

댓글

티스토리툴바